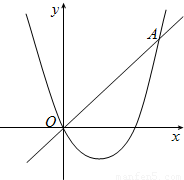
摘要：已知抛物线与直线:的交点除了原点外.还相交于另一点. (1)分别求出这个抛物线的顶点.点的坐标(可用含的式子表示), (2)将抛物线沿着轴对折(翻转)后.得到的图象叫做“新抛物线 .则: ①当时.求这个“新抛物线 的解析式.并判断这个“新抛物线 的顶点是否在直线上, ②在①的条件下.“新抛物线 上是否存在一点.使点到直线的距离等于线段的?若存在.请直接写出满足条件的点坐标,若不存在.请说明理由.
网址：http://m.1010jiajiao.com/timu3_id_448113[举报]
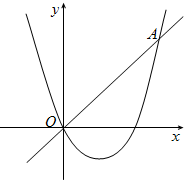已知抛物线y=ax2-2ax与直线l：y=ax（a＞0）的交点除了原点O外，还相交于另一点A．（1）分别求出这个抛物线的顶点、点A的坐标（可用含a的式子表示）；
（2）将抛物线y=ax2-2ax沿着x轴对折（翻转180°）后，得到的图象叫做“新抛物线”，则：①当a=1时，求这个“新抛物线”的解析式，并判断这个“新抛物线”的顶点是否在直线l上；②在①的条件下，“新抛物线”上是否存在一点P，使点P到直线l的距离等于线段OA的
| 1 | 24 |
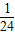？若存在，请直接写出满足条件的点P坐标；若不存在，请说明理由．
