摘要：证明:(1)∵AE⊥BD.∴=.∴∠EBD=∠ECB.∵∠ABH=∠DBH.∠BHE=∠ECB+∠CBH.∠HBE=∠DBH+∠EBD.∴∠BHE=∠HBE. ∴BE=HE. 解: (2)连结QC.TB.则∠BCQ+∠CBQ=90°.又∠BDQ+∠ATD=90°.而∠BCQ=∠BDQ.∴∠CBQ=∠ATD=∠ATB.∴ΔABG∽ΔATB.∴AB2=AG•AT.∵AH⊥CE.∴H为CE的中点.∴BE=EC.∴ΔBEO∽ΔCBE.∴==. 设⊙A的半径为R.由AB2-OA2=BO2.OE=R-3.得R2-32=4(R-3)2.解得.R=5.或R=3.∴AT•AG=AB2=25. (方法二提示:可连结AD,CD证ΔBAG∽ΔTAD) (3)答:②的值不变. 证明:作O1K⊥MN于K.连结O1N.PN.BM. 则MN=2NK. 且∠N O1K=∠NPM. ∴==2sin∠NO1K=2sin∠NPM. 由直线y=x+3 得 OB=OD=4.OM⊥BD. ∴∠BMO=∠DMO. 又∠BMO=∠ABM+∠BAM.∠DMO=∠MPN+∠PNM. ∵∠ABM=∠PNM. ∴∠MPN=∠BAM=∠NO1K.=2sin∠BAM=2×= . 所以的值不变.其值为 .
网址：http://m.1010jiajiao.com/timu3_id_448112[举报]
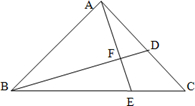24、如图，在Rt△ABC中，∠BAC=90°，AB=AC，BD是AC边上的中线，AE⊥BD于F，交BC于E．（1）证明：∠ABD=∠DAF；
（2）试判断∠ADB与∠CDE的大小关系，并证明你的结论．
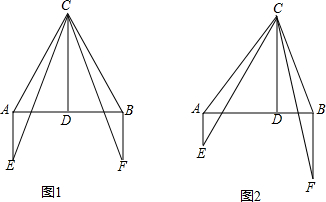
（2012•顺义区二模）已知：如图，D为线段AB上一点（不与点A、B重合），CD⊥AB，且CD=AB，AE⊥AB，BF⊥AB，且AE=BD，BF=AD．
（1）如图1，当点D恰是AB的中点时，请你猜想并证明∠ACE与∠BCF的数量关系；
（2）如图2，当点D不是AB的中点时，你在（1）中所得的结论是否发生变化，写出你的猜想并证明；
（3）若∠ACB=α，直接写出∠ECF的度数（用含α的式子表示）．
查看习题详情和答案>>
（1）如图1，当点D恰是AB的中点时，请你猜想并证明∠ACE与∠BCF的数量关系；
（2）如图2，当点D不是AB的中点时，你在（1）中所得的结论是否发生变化，写出你的猜想并证明；
（3）若∠ACB=α，直接写出∠ECF的度数（用含α的式子表示）．
24、将两个全等的直角三角形ABC和DEC，按如图1方式放置．其中，∠ABC=∠DEC=90°，AB与DE交于点O．
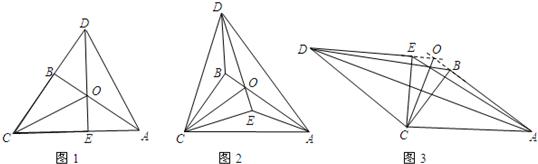
（1）通过观察和测量，猜想AE、BD的数量关系为
（2）将三角形DEC绕点C逆时针旋转至图2所示的位置，（1）中的猜想是否还成立，若成立，请证明；不成立，请说明理由．
（3）将三角形DEC绕点C继续旋转至图3所示的位置，（1）中的猜想是否还成立（直接写出结论，不需证明）．
查看习题详情和答案>>
（1）通过观察和测量，猜想AE、BD的数量关系为
AE=BD
；CO与AD的位置关系是CO⊥AD
；（2）将三角形DEC绕点C逆时针旋转至图2所示的位置，（1）中的猜想是否还成立，若成立，请证明；不成立，请说明理由．
（3）将三角形DEC绕点C继续旋转至图3所示的位置，（1）中的猜想是否还成立（直接写出结论，不需证明）．
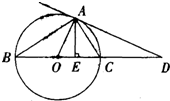23、如图，AD切⊙O于点A，直径BC，交AD于D，AE⊥BD于E．请根据图形将线段成比例的式子写出来（至少写出4个．一个比例式和由它变形得出的比例式按一个计算）．并证明其中的一个比例式成立．
28、如图，已知AC⊥AB，DB⊥AB，AC=BE，AE=BD，试猜想线段CE与DE的大小与位置关系，并证明你的结论．