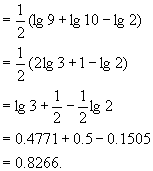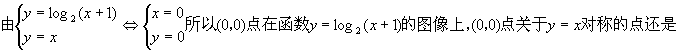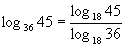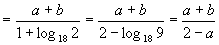0 446628 446636 446642 446646 446652 446654 446658 446664 446666 446672 446678 446682 446684 446688 446694 446696 446702 446706 446708 446712 446714 446718 446720 446722 446723 446724 446726 446727 446728 446730 446732 446736 446738 446742 446744 446748 446754 446756 446762 446766 446768 446772 446778 446784 446786 446792 446796 446798 446804 446808 446814 446822 447348
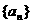 中,已知
中,已知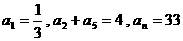 ,则
,则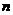 为( )
为( )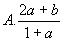
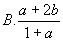
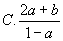
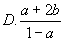
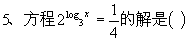
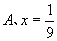
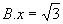
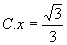
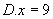
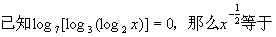 ( )
( ) 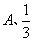
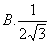
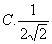
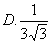
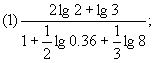
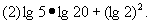
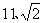
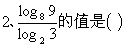
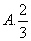 B、1
B、1
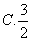 D、2
D、2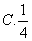 D、4
D、4 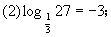 (3)54=625;
(3)54=625; 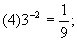
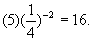
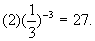
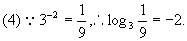
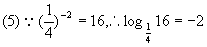
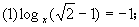
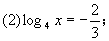
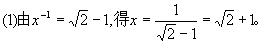
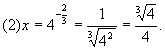
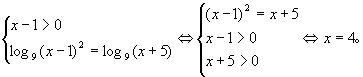
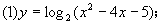
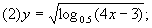
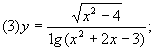
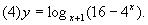
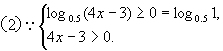
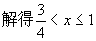
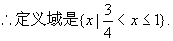
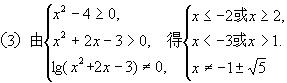
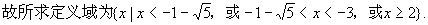

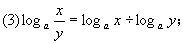
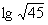 。
。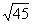 的常用对数分解为2,3的常用对数代入计算。
的常用对数分解为2,3的常用对数代入计算。