0 446698 446706 446712 446716 446722 446724 446728 446734 446736 446742 446748 446752 446754 446758 446764 446766 446772 446776 446778 446782 446784 446788 446790 446792 446793 446794 446796 446797 446798 446800 446802 446806 446808 446812 446814 446818 446824 446826 446832 446836 446838 446842 446848 446854 446856 446862 446866 446868 446874 446878 446884 446892 447348
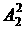 ;(2)
;(2) ;(3)144
;(3)144 =15(种)
=15(种)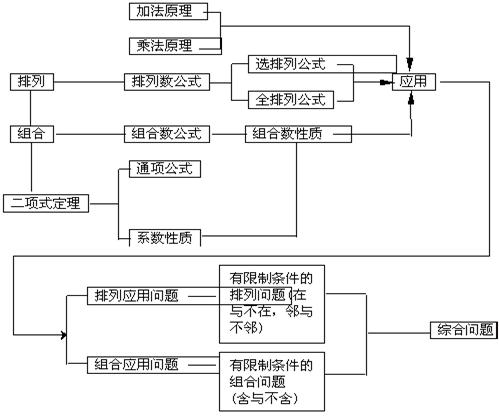
 如图,
如图,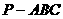 是底面边长为
是底面边长为 的正三棱锥,
的正三棱锥, 、
、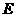 、
、 分别为棱
分别为棱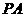 、
、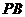 、
、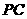 上的点,截面
上的点,截面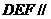 底面
底面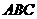 ,且棱台
,且棱台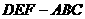 与棱锥
与棱锥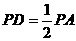 ,求二面角
,求二面角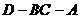 的大小;(结果用反三角函数值表示)
的大小;(结果用反三角函数值表示)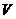 ,是否存在体积为
,是否存在体积为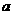 的正方形剪去图中的阴影部分,沿图中所画虚线折成一个正三棱锥。这个正三棱锥侧棱与底面所成角的余弦值是
的正方形剪去图中的阴影部分,沿图中所画虚线折成一个正三棱锥。这个正三棱锥侧棱与底面所成角的余弦值是
 的二面角内,放一个半径为
的二面角内,放一个半径为 的球切两半平面于
的球切两半平面于 、
、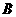 两点,那么这两个切点在球面上最短距离是
两点,那么这两个切点在球面上最短距离是  已知球的表面积为
已知球的表面积为 ,有两个平行截面的面积分别为
,有两个平行截面的面积分别为 和
和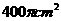 ,则这两个平行截面间的距离是
,则这两个平行截面间的距离是