5.已知函数f(x)
= lg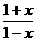 的定义域为A,函数g(x)=lg(1+x) – lg(1-x)的定义域为B,则下述关于A、B关系不正确的为
( )
的定义域为A,函数g(x)=lg(1+x) – lg(1-x)的定义域为B,则下述关于A、B关系不正确的为
( )
A.AÊB B.A∪B=B C.A∩B=B D.B(≠A
[讲练平台]
例1 求函数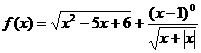 的定义域.
的定义域.
分析 根据有关条件列出不等式组,再求出不等式组的解集即为所求函数的定义域.
解 由函数解析式有意义,得
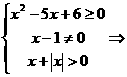 Þ0<x<1或1<x≤2,或x≥3.
Þ0<x<1或1<x≤2,或x≥3.
故函数的定义域是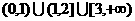 .
.
点评 (1)求以解析式给出的函数定义域时,应遵循以下几条原则:①分式的分母不为零;②偶次根号下被开方数非负;③在a°中底数a≠0;④若f(x)是由几个部分构成的,则应采用交集法;⑤实际问题结合变量的实际意义来确定,等等;
(2)求不等式组的解集,通常借助数轴的直观性;
(3)函数的定义域一般应用集合或区间形式表示,在用区间表示时,要弄清区间端点的归属,正确使用开区间和闭区间符号,需特别注意的是,“∞”不是一个确定的数,而是一个变化趋势,只能用开区间;
(4)必须把所有的限制条件都列出来,特别是在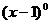 中,x-1≠0,不能遗漏.
中,x-1≠0,不能遗漏.
例2 若函数 y=lg(x2+ax+1)的定义域为R,求实数a的取值范围.
分析 由函数 y=lg(x2+ax+1)的定义域为R知:x2+ax+1>0对x∈R恒成立,而f(x)= x2+ax+1为二次函数,函数值恒正,故可利用“△”法求解.
解 因函数 y=lg(x2+ax+1)的定义域为R,故x2+ax+1>0对x∈R恒成立,而f(x)= x2+ax+1是开口向上的抛物线,从而△<0,即a2-4<0,解得 -2<a<2,它便是所求的a的取值范围.
点评 (1)“△”法可判断一元二次函数值恒正、恒负或非正、非负;
(2)必须注意所用△的值是大于零、小于零、还是不大于零、不小于零.如下面的问题:关于x的不等式x2+ax+1<0的解集为 ,试求实数a的取值范围.问题便等价于x2+ax+1≥0的解集为R,从而有△≤0,解得 –2≤a≤2.
,试求实数a的取值范围.问题便等价于x2+ax+1≥0的解集为R,从而有△≤0,解得 –2≤a≤2.
变题1 已知函数 y=lg(x2+ax+1)的值域为R,求a的取值范围.
提示:利用△≥0Þ a≥2或a≤-2.
变题2 已知函数 y=lg(ax2+ax+1)的定义域为R,求a的取值范围.
提示:分a>0与a=0的两种情况求解,其答案为0≤a<4.
思考:变题1、变题2及原题,它们的区别何在?
例3 《中华人民共和国个人所得税法》第十四条中有下表:
个人所得税税率表一(工资、薪金所得适用)
|
级别 |
全月应纳税所得额 |
税率(%) |
|
1 2 3 4 5 6 7 8 9 |
不超过500元部分 超过500元至2000元部分 超过2000元至5000元部分 超过5000元至20000元部分 超过20000元至40000元部分 超过40000元至60000元部分 超过60000元至80000元部分 超过80000元至10000元部分 超过100000元部分 |
5 10 15 20 25 30 35 40 45 |
表中“全月应纳税所得额”是从月工资、薪金收入中减去1000元后的余额.例如某人月工资、薪金收入1220元,减除1000元,应纳税所得额就是220元,应缴纳个人所得税11元.
(1)请写出月工资、薪金的个人所得y关于收入额x(0<x≤3000)的函数表达式;
(2)一公司职员某月缴纳个人所得税75元,问他该月工资、薪金的收入多少?
分析 先读懂题意,正确理解“全月应纳税所得额”等的意义,然后利用分段函数法列出个人所得y关于收入额x的函数关系式,利用该关系式继续求解其它的问题.
解 (1)当0<x≤1000时,y=x;
当1000<x≤1500时,扣税: (x-1000) ·5%,从而所得为
y=x- (x-1000) ·5% = 0.95x+50;
当1500<x≤3000时,扣税: (x-1500)·10%+500 ·5% = 0.1x-125,从而所得为
y= x-(0.1x-125) =0.9x+125.
故 y =
(2)显然,该职员的工资、薪金x满足1500<x≤3000,故由
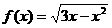 的定义域为
( )
的定义域为
( )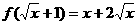 ,求f(x+1).
,求f(x+1). )=x,求f(x).
)=x,求f(x).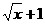 )为整体,采用换元法或配方法可求得f(x)的解析式,再用(x+1)整体代换f(x)中的x,即可求出f(x+1)的解析式;
)为整体,采用换元法或配方法可求得f(x)的解析式,再用(x+1)整体代换f(x)中的x,即可求出f(x+1)的解析式;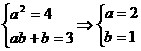 或
或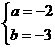 ,∴ f(x)=2x+1或f(x)= -2x-3.
,∴ f(x)=2x+1或f(x)= -2x-3.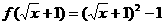 ,∴ f(x)=x2-1 (x≥1),
,∴ f(x)=x2-1 (x≥1),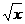 = t-1,∴f(t)=
(t-1)2+2(t-1)= t2-1.
= t-1,∴f(t)=
(t-1)2+2(t-1)= t2-1. .
.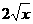 +3 D.
+3 D.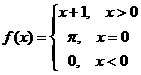 ,则f{f[f(-1)]}= .
,则f{f[f(-1)]}= .