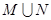网址:http://m.1010jiajiao.com/timu3_id_4465888[举报]
已知函数![]() 的定义域为
的定义域为![]() 且
且![]() ,对任意
,对任意![]() 都有
都有![]()
![]()
数列![]() 满足
满足![]() N
N![]() .证明函数
.证明函数![]() 是奇函数;求数列
是奇函数;求数列![]() 的通项公式;令
的通项公式;令![]() N
N![]() , 证明:当
, 证明:当![]() 时,
时,![]() .
.
(本小题主要考查函数、数列、不等式等知识, 考查化归与转化、分类与整合的数学思想方法,以及抽象概括能力、推理论证能力、运算求解能力和创新意识)
查看习题详情和答案>>设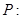 关于
关于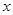 的不等式,
的不等式,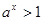 的解集是
的解集是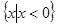 ,
,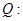 函数
函数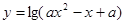 的定义域为
的定义域为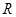 。若“
。若“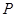 或
或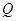 ”为真,“
”为真,“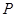 且
且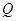 ”为假,求
”为假,求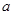 的取值范围。
的取值范围。
【解析】本试题主要考查了命题的真智慧以及不等式的解集的综合运用。利用
若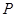 真则
真则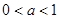
若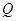 真,则
真,则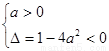 得
得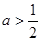
“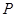 或
或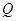 ”为真,“
”为真,“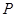 且
且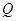 ”为假,则
”为假,则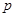 、
、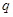 一真一假分类讨论得到。
一真一假分类讨论得到。
若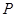 真则
真则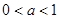
若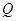 真,则
真,则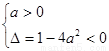 得
得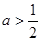 ……………………6分
……………………6分
“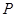 或
或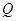 ”为真,“
”为真,“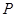 且
且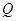 ”为假,则
”为假,则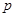 、
、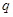 一真一假
一真一假
当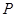 真
真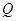 假时
假时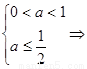
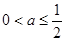 ………………………………9分
………………………………9分
当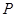 假
假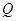 真时
真时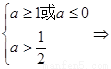
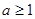 ………………………………12分
………………………………12分
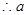 的取值范围为
的取值范围为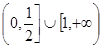
查看习题详情和答案>>
已知函数f(x)= ,
, 为常数。
为常数。
(I)当 =1时,求f(x)的单调区间;
=1时,求f(x)的单调区间;
(II)若函数f(x)在区间[1,2]上为单调函数,求 的取值范围。
的取值范围。
【解析】本试题主要考查了导数在研究函数中的运用。第一问中,利用当a=1时,f(x)= ,则f(x)的定义域是
,则f(x)的定义域是 然后求导,
然后求导, ,得到由
,得到由 ,得0<x<1;由
,得0<x<1;由 ,得x>1;得到单调区间。第二问函数f(x)在区间[1,2]上为单调函数,则
,得x>1;得到单调区间。第二问函数f(x)在区间[1,2]上为单调函数,则 或
或 在区间[1,2]上恒成立,即即
在区间[1,2]上恒成立,即即 ,或
,或 在区间[1,2]上恒成立,解得a的范围。
在区间[1,2]上恒成立,解得a的范围。
(1)当a=1时,f(x)= ,则f(x)的定义域是
,则f(x)的定义域是
 。
。
由 ,得0<x<1;由
,得0<x<1;由 ,得x>1;
,得x>1;
∴f(x)在(0,1)上是增函数,在(1, 上是减函数。……………6分
上是减函数。……………6分
(2) 。若函数f(x)在区间[1,2]上为单调函数,
。若函数f(x)在区间[1,2]上为单调函数,
则 或
或 在区间[1,2]上恒成立。∴
在区间[1,2]上恒成立。∴ ,或
,或 在区间[1,2]上恒成立。即
在区间[1,2]上恒成立。即 ,或
,或 在区间[1,2]上恒成立。
在区间[1,2]上恒成立。
又h(x)= 在区间[1,2]上是增函数。h(x)max=(2)=
在区间[1,2]上是增函数。h(x)max=(2)= ,h(x)min=h(1)=3
,h(x)min=h(1)=3
即
 ,或
,或 。 ∴
。 ∴
 ,或
,或 。
。
查看习题详情和答案>>
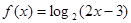 的定义域为集合M,函数
的定义域为集合M,函数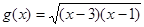 的定义域为集合N.求:
的定义域为集合N.求: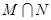 ,
,