0 446498 446506 446512 446516 446522 446524 446528 446534 446536 446542 446548 446552 446554 446558 446564 446566 446572 446576 446578 446582 446584 446588 446590 446592 446593 446594 446596 446597 446598 446600 446602 446606 446608 446612 446614 446618 446624 446626 446632 446636 446638 446642 446648 446654 446656 446662 446666 446668 446674 446678 446684 446692 447348
 ,an+1= f(an)(nÎN*),求证:当n≥2时,
,an+1= f(an)(nÎN*),求证:当n≥2时, .
.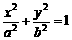 (a﹥b﹥0),曲线C2方程为
(a﹥b﹥0),曲线C2方程为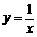 ,且曲线C1与C2在第一象限内只有一个公共点P.
,且曲线C1与C2在第一象限内只有一个公共点P.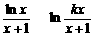 成立,求实数k的取值范围.
成立,求实数k的取值范围.
 如图,四棱锥P–ABCD中,PD⊥面ABCD,PA与平面ABCD所成的角为60°,在四边形ABCD中,∠D=∠DAB=90°,AB=4,CD=1,AD=2,(1)求异面直线PA与BC所成的角;(2)若PB的中点为M,求证:平面AMC⊥平面PBC.
如图,四棱锥P–ABCD中,PD⊥面ABCD,PA与平面ABCD所成的角为60°,在四边形ABCD中,∠D=∠DAB=90°,AB=4,CD=1,AD=2,(1)求异面直线PA与BC所成的角;(2)若PB的中点为M,求证:平面AMC⊥平面PBC. . 求:
. 求: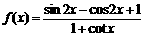 ,(1)化简f(x);(2)若
,(1)化简f(x);(2)若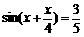 ,且
,且 ,求f(x)的值.
,求f(x)的值. ,则甲、乙两地球面距离为
.
,则甲、乙两地球面距离为
.