0 446420 446428 446434 446438 446444 446446 446450 446456 446458 446464 446470 446474 446476 446480 446486 446488 446494 446498 446500 446504 446506 446510 446512 446514 446515 446516 446518 446519 446520 446522 446524 446528 446530 446534 446536 446540 446546 446548 446554 446558 446560 446564 446570 446576 446578 446584 446588 446590 446596 446600 446606 446614 447348
 =(cos
=(cos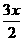 ,sin
,sin =(cos
=(cos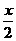 ,-sin
,-sin ,
, ].
]. 及
及 ;
;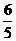 <
<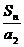 <
<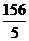 ,求n的值.
,求n的值. 中,
中, 、
、 、
、 ,
, .现将坐标平面沿
.现将坐标平面沿 轴折成直二面角,记
轴折成直二面角,记 中点为
中点为 ,如图所示.
,如图所示. .
. 是异面直线
是异面直线 与
与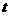 的值及直线
的值及直线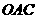 所成的角.
所成的角.
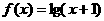 ,点
,点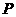 是函数
是函数 图像上的任意一点,点
图像上的任意一点,点 的轨迹是函数
的轨迹是函数 的图像当
的图像当 时,总有
时,总有 恒成立.
恒成立. 的取值范围.
的取值范围.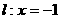 ,点B是l上的动点,若过B垂直于y轴的直线与线段BF的垂直平分线交于点M.
,点B是l上的动点,若过B垂直于y轴的直线与线段BF的垂直平分线交于点M. 的最小值是 .
的最小值是 .  、
、 、
、 、
、 、
、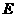 五名学生参加网页设计竞赛,决出了第一到第五的名次,
五名学生参加网页设计竞赛,决出了第一到第五的名次, ,
, .
.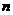 个向量
个向量 存在
存在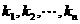 ,使得
,使得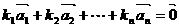 成立,则称向量
成立,则称向量 ,
, ,
,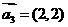 “线性相关”的实数
“线性相关”的实数 依次可以
依次可以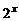 ,则f -1(
,则f -1( )=
)= (B)-1 (C)
(B)-1 (C)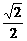 (D)
(D)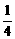
 ,则集合
,则集合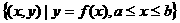
 中含有元素的个数为
中含有元素的个数为
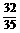 (B)
(B)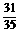 (C)
(C)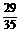 (D)
(D)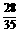
 ,则z=x+y的最大值为
,则z=x+y的最大值为
 ,
, 互相平行的一个充分条件是
互相平行的一个充分条件是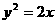 (
( )上,并且与抛物线
)上,并且与抛物线 (B)
(B)
 (D)
(D)
 (C)
(C) (D)
(D)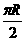
 ,则其离心率为
,则其离心率为 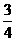 (B)
(B) (C)
(C)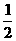 (D)
(D)
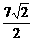 (B)
(B)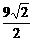 (C)
(C) (D)
(D)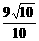
 满足对任意的实数
满足对任意的实数 ,则当函数
,则当函数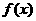 取最小值时
取最小值时 (B)
(B)
 (D)
(D)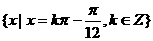
 ,都有
,都有 ,设
,设 ,问数列{
,问数列{ }中,值不同的项至多有
}中,值不同的项至多有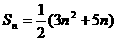 ,数列{bn}中, b3=4, b6=32.
,数列{bn}中, b3=4, b6=32. 的所有项之和;
的所有项之和; )是数列{an}和{bn}的所有相同项(排列顺序不变)组成的数列,求{cn}的
)是数列{an}和{bn}的所有相同项(排列顺序不变)组成的数列,求{cn}的 )上的增函数,且对一切x>0,满足f
)上的增函数,且对一切x>0,满足f 
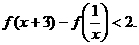
 sin2x+a (a
sin2x+a (a R为常数) .
R为常数) . 时, f (x)的最大值为4,求a的值.
时, f (x)的最大值为4,求a的值.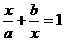 ,其中a、b为实数.
,其中a、b为实数. (i为虚数单位)是该方程的根,求a、b的值;
(i为虚数单位)是该方程的根,求a、b的值; 时, 证明该方程没有实数根.
时, 证明该方程没有实数根.