0 446552 446560 446566 446570 446576 446578 446582 446588 446590 446596 446602 446606 446608 446612 446618 446620 446626 446630 446632 446636 446638 446642 446644 446646 446647 446648 446650 446651 446652 446654 446656 446660 446662 446666 446668 446672 446678 446680 446686 446690 446692 446696 446702 446708 446710 446716 446720 446722 446728 446732 446738 446746 447348
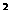 -c
-c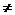 0
0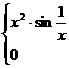
 ,
在x=0处的导数。
,
在x=0处的导数。
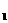 、F
、F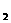 分别是双曲线
分别是双曲线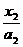 -
-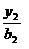 =1的左、右焦点,过F
=1的左、右焦点,过F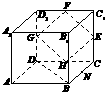 如图,在正四棱柱ABCD-A
如图,在正四棱柱ABCD-A b;③若a=e
b;③若a=e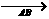 =
=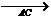 =2
=2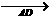 .其中,正确命题的序号是
.
.其中,正确命题的序号是
.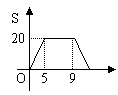 ①ABCD是梯形;
①ABCD是梯形; x
x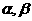 是方程f(x)=0的两根,实数a、b、
是方程f(x)=0的两根,实数a、b、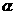 、
、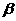 的大小关系可能是
的大小关系可能是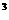
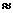 1.069,则3年后两人所得的利息(不计利息税)
1.069,则3年后两人所得的利息(不计利息税)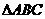 中,
中,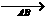 ·
·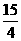 ,|
,|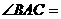
 B.60
B.60