(17)(本小题满分12分)
制造某种零件,甲机床的废品率为0.04,乙机床的废品率为0.05,从这二机床生产的产品中各抽出一件作检验,求
(Ⅰ)其中恰有一件废品的概率;
(Ⅱ)其中至多有一件废品的概率;
(Ⅲ)其中没有废品的概率.
(18)(本小题满分12分)
数列 的前n项的和为
的前n项的和为 ,且
,且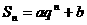 .其中
.其中 ,
,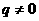 ,
, .
.
(Ⅰ)若数列 是公比为q的等比数列,求证
是公比为q的等比数列,求证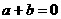 ;
;
(Ⅱ)若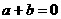 ,求证数列
,求证数列 是等比数列.
是等比数列.
(19)(本小题满分12分)
正方体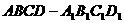 中,E、F分别为AB、BB1的中点(如图综10).
中,E、F分别为AB、BB1的中点(如图综10).
(Ⅰ)证明EF∥平面 ;
;
(Ⅱ)求二面角 的平面角的正切值;
的平面角的正切值;
(Ⅲ)若 ,求三棱锥
,求三棱锥 的体积.
的体积.

综10
(20)(本小题满分12分)
已知函数 .
.
(Ⅰ)求此函数的定义域及单调递增区间;
(Ⅱ)求此函数的极大值和极小值.
(21)(本小题满分12分)
已知甲、乙、丙三种食品的维生素A、B的含量及成本如下表:
|
|
甲 |
乙 |
丙 |
|
维生素A含量(单位/千克) |
600 |
700 |
400 |
|
维生素B含量(单位/千克) |
800 |
400 |
500 |
|
成本(元/千克) |
11 |
9 |
4 |
某食品研究所想用x千克甲种食品、y千克乙种食品、z千克丙种食品配制成100千克的混合食品,并使混合食品中至少含有56000单位的维生素A、63000单位的维生素B.
(Ⅰ)用x、y表示这种混合食品的总成本C(元);
(Ⅱ)确定x、y、z的值,使混合食品的总成本最低.
(22)(本小题满分14分)
已知双曲线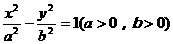 的左、右两个顶点分别为A、B,过这双曲线右焦点F2且与x轴垂直的直线交双曲线于两点P、Q、P在x轴上方,且
的左、右两个顶点分别为A、B,过这双曲线右焦点F2且与x轴垂直的直线交双曲线于两点P、Q、P在x轴上方,且 ,
,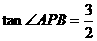 .
.
(Ⅰ)求这双曲线的方程;
(Ⅱ)若直线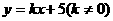 与双曲线交于不同两点M、N,且M、N都在以E(0,-1)为圆心的同一个圆上,求k的值.
与双曲线交于不同两点M、N,且M、N都在以E(0,-1)为圆心的同一个圆上,求k的值.
 ,
, ,
, },求
},求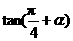 的值.
的值.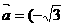 ,
, ),
), ,
, ),求
),求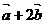 与
与 的夹角
的夹角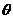 的值.
的值.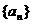 中,
中,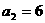 ,
,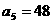 ,求
,求 及前6项和
及前6项和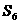 .
.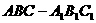 中,
中,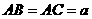 ,
,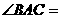 90°,顶点
90°,顶点 在底面ABC上的射影为BC边的中点M.
在底面ABC上的射影为BC边的中点M.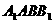 与平面ABC所成的二面角为60°,求三棱柱
与平面ABC所成的二面角为60°,求三棱柱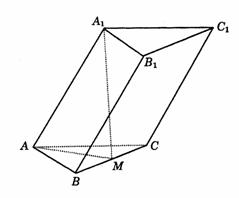
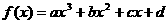 的图象与y轴的交点为P,且曲线在P点处的切线方程为
的图象与y轴的交点为P,且曲线在P点处的切线方程为 .若函数
.若函数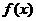 在x=2处取得极小值-16.
在x=2处取得极小值-16. 的离心率
的离心率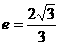 ,过点A(0,-b)和B(a,0)的直线与原点间的距离为
,过点A(0,-b)和B(a,0)的直线与原点间的距离为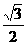 .
.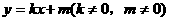 与双曲线交于两个不同的点C、D,并且C、D两点都在以A为圆心的同一个圆上,求实数m的取值范围.
与双曲线交于两个不同的点C、D,并且C、D两点都在以A为圆心的同一个圆上,求实数m的取值范围. 与两坐标轴所构成的三角形的面积为
与两坐标轴所构成的三角形的面积为 ,则
,则 =________.
=________. =________.
=________. ,那么z的三角形式是________.
,那么z的三角形式是________. ,
,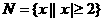 ,则(
,则(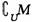 )∪(
)∪( )=( ).
)=( ). B.
B.
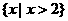 D.
D.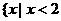 或
或
 是( ).O
是( ).O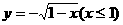 的反函数是( ).
的反函数是( ). B.
B.
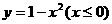 D.
D.
 的准线方程是( ).
的准线方程是( ).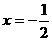 B.
B.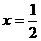 C.
C. D.
D.
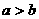 ,
, ,则下列不等式中一定成立的是( ).
,则下列不等式中一定成立的是( ).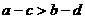 B.
B.
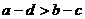 D.
D.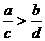
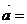 (1,1),
(1,1), (1,-1),
(1,-1), (-1,2),则
(-1,2),则 B.
B.
 D.
D.
 的展开式中,常数项是( ).
的展开式中,常数项是( ). B.
B.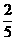 C.
C. D.
D.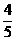
 在点
在点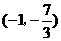 处的切线的倾斜角是( ).
处的切线的倾斜角是( ). 中,若
中,若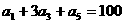 ,则
,则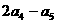 =( ).
=( ). 中,M、N分别是侧棱PB、PC的中点,若截面
中,M、N分别是侧棱PB、PC的中点,若截面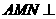 侧面PBC,则此三棱锥的侧棱与底面所成角的正切值是( ).
侧面PBC,则此三棱锥的侧棱与底面所成角的正切值是( ).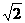 C.
C.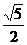 D.
D.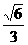
 的一个焦点到一条渐近线的距离为
的一个焦点到一条渐近线的距离为 ,则a=________.
,则a=________. ,则a=________.
,则a=________. ;
②△
;
②△ 是等边三角形;
是等边三角形;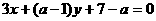 和
和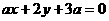 平行且不重合的( ).
平行且不重合的( ).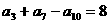 ,
, ,那么其前13项的和
,那么其前13项的和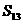 等于( ).
等于( ).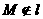 ,那么经过点M且与直线l相切的动圆的圆心的轨迹是( ).
,那么经过点M且与直线l相切的动圆的圆心的轨迹是( ).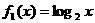 ,
,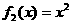 ,
,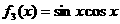 ,
,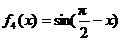 .从中任取两个相乘得到若干个函数,所得这些函数中偶函数共有( ).
.从中任取两个相乘得到若干个函数,所得这些函数中偶函数共有( ). 、
、 的夹角为90°,且
的夹角为90°,且 ,记
,记 ,
, ,若
,若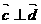 ,则k=( ).
,则k=( ). 上移动,PA、PB是圆
上移动,PA、PB是圆 的两条切线,A、B是切点,O是原点,则四边形PAOB的面积最小值为( ).
的两条切线,A、B是切点,O是原点,则四边形PAOB的面积最小值为( ). 上移动时,过点P曲线的切线的倾斜角的取值范围是( ).
上移动时,过点P曲线的切线的倾斜角的取值范围是( ). ,
, ]
B.[
]
B.[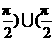 ,
, D.
D. ,p )
,p )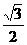 B.
B.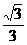 C.
C. D.
D.
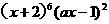 的展开式中,
的展开式中, 项的系数为100,那么实数a的值为( ).
项的系数为100,那么实数a的值为( ). B.
B. 或
或 C.0或
C.0或 是由正数组成的等比数列,且
是由正数组成的等比数列,且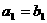 .若存在自然数m,使得
.若存在自然数m,使得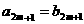 ,则必有( ).
A.
,则必有( ).
A. B.
B.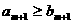
 D.
D.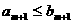
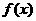 的二次项系数为正数,且对任意
的二次项系数为正数,且对任意 R都有
R都有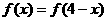 成立,若
成立,若 ,则x的取值范围是( ).
,则x的取值范围是( ). B.
B. 或
或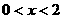
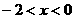 D.
D.