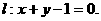0 446588 446596 446602 446606 446612 446614 446618 446624 446626 446632 446638 446642 446644 446648 446654 446656 446662 446666 446668 446672 446674 446678 446680 446682 446683 446684 446686 446687 446688 446690 446692 446696 446698 446702 446704 446708 446714 446716 446722 446726 446728 446732 446738 446744 446746 446752 446756 446758 446764 446768 446774 446782 447348
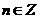 },B={x|x=4n-3,
},B={x|x=4n-3,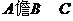 B、
B、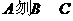 C、
C、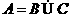 D、
D、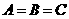
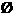 {1,2,3,4,5},且当
{1,2,3,4,5},且当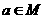 时,也有6-
时,也有6-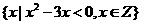 ,A
,A B={1},则A
B={1},则A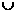 B等于( )
B等于( )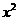 -4ax-5
-4ax-5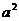 >0的解集是( )
>0的解集是( )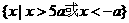 B、
B、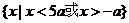
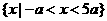 D、
D、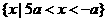
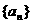 的前n项和记为Sn,已知
的前n项和记为Sn,已知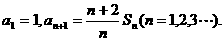 证明:
证明: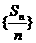 是等比数列;
是等比数列;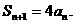
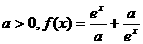 是R上的偶函数.
是R上的偶函数.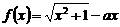 ,其中
,其中 。
。 ;
;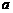 的取值范围,使函数
的取值范围,使函数 在区间
在区间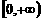 上是单调函数。
上是单调函数。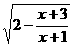 的定义域为A, g(x)=lg[(x-a-1)(2a-x)](a<1)
的定义域为B.
的定义域为A, g(x)=lg[(x-a-1)(2a-x)](a<1)
的定义域为B. A, 求实数a的取值范围.
A, 求实数a的取值范围.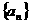 是由非负整数组成的数列,满足
是由非负整数组成的数列,满足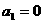 ,
,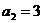 ,
,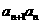 =
=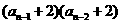 ,
,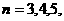 ……。
……。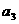 ;
;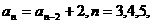 ……;
……; 项和
项和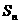 。
。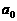 为常数,且
为常数,且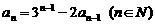 .
.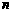 ≥1,
≥1,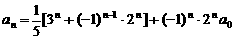 ;
;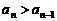 ,求
,求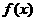 和数列
和数列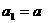 ,
,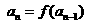 (n=2,3,4,…),
(n=2,3,4,…),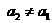 ,
,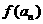 -
-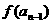 =
=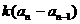 (n=2,3,4,…),其中a为常数,k为非零常数。
(n=2,3,4,…),其中a为常数,k为非零常数。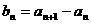
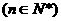 ,证明数列
,证明数列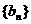 是等比数列;
是等比数列; 时,求
时,求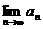 。
。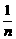 14、1
15、(0,0)、(1,1) 16、
14、1
15、(0,0)、(1,1) 16、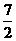
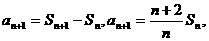
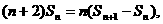 整理得
整理得 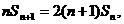
 故
故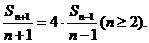 于是
于是 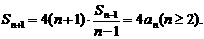
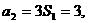 故
故 
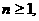 都有
都有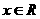 有
有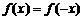 ,即
,即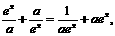
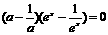 对一切
对一切 即a2=1.
即a2=1. 
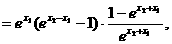
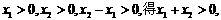
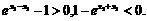
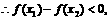 即f(x)在(0,+∞)上是增函数.
即f(x)在(0,+∞)上是增函数. 得
得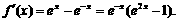
 时,有
时,有 此时
此时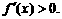
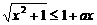 ,
,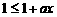 ,即
,即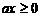 ,其中常数
,其中常数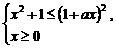 即
即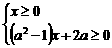 --3分
--3分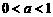 时,所给不等式的解集为
时,所给不等式的解集为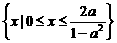 ;
;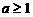 时,所给不等式的解集为
时,所给不等式的解集为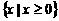 。--6分
。--6分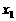 ,
,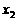 ,使得
,使得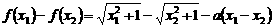
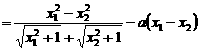
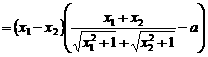 。--8分
。--8分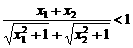 ,∴
,∴ 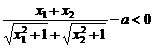 ,
,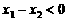 ,∴
,∴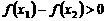 ,即
,即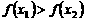 。
。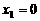 ,
,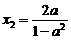 ,满足
,满足 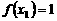 ,
,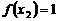 ,即
,即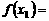
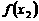 ,所以函数
,所以函数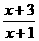 ≥0, 得
≥0, 得 ≥0, x<-1或x≥1
≥0, x<-1或x≥1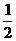 或a≤-2, 而a<1,
或a≤-2, 而a<1, ,且
,且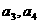 均为非负整数,所以
均为非负整数,所以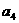 =10,
=10,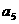 =
=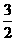 ,与题设矛盾。
,与题设矛盾。 ,与题设矛盾。
,与题设矛盾。 ,
,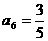 ,与题设矛盾。
,与题设矛盾。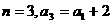 ,等式成立。
,等式成立。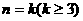 时等式成立,即
时等式成立,即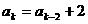 ,
,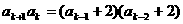
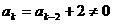
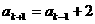
 时,等式
时,等式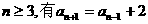 。
。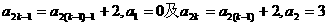 得
得 ……。
……。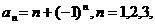 ……。
……。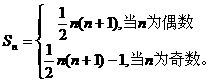
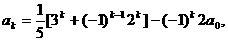
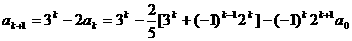
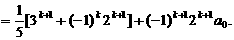
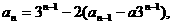 用
用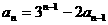 代入,可解出
代入,可解出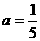 .
. 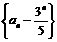 是公比为-2,首项为
是公比为-2,首项为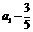 的等比数列.
的等比数列. 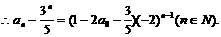 即
即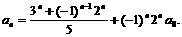
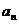 通项公式
通项公式 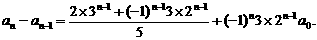
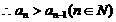 等价于
等价于 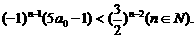 ……①
……①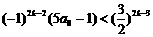
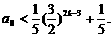 ……②
……②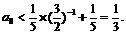
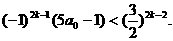
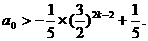 ……③
③式对k=1,2,…都成立,有
……③
③式对k=1,2,…都成立,有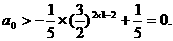 综上,①式对任意n∈N*,成立,有
综上,①式对任意n∈N*,成立,有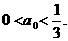
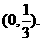
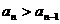 (n∈N*)成立,特别取n=1,2有
(n∈N*)成立,特别取n=1,2有 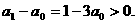
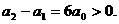 因此
因此 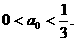 下面证明当
下面证明当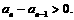 由an的通项公式
由an的通项公式 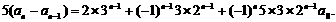
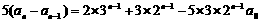


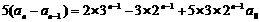
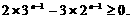
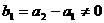 ,可得
,可得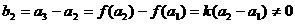 。
。
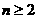 时
时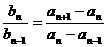

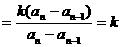

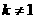 时,
时,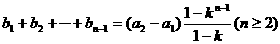
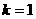 时,
时,
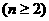 。
。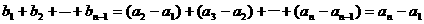
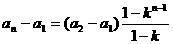
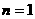 也成立。所以,数列
也成立。所以,数列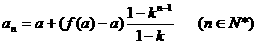
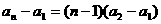
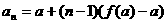

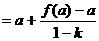
 是首项为1的正项数列,且
是首项为1的正项数列,且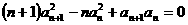 (
(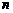 =1,2,3,…),则它的通项公式是
=1,2,3,…),则它的通项公式是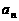 =
。
=
。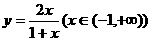 图象与其反函数图象的交点坐标为_ __。
图象与其反函数图象的交点坐标为_ __。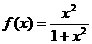 ,那么
,那么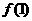 +
+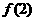 +
+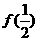 +
+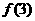 +
+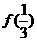 +
+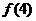 +
+ 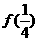 =
。
=
。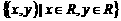 ,映射
,映射 把集合A中的元素
把集合A中的元素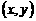 映射成集合B中的元素
映射成集合B中的元素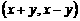 ,则在映射
,则在映射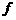 下,象
下,象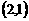 的原象是( )
的原象是( )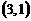 (B)
(B)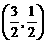 (C)
(C)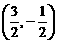 (D)
(D)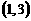
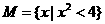 ,
,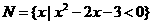 ,则集合
,则集合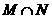 =( )
=( ) }
B.{
}
B.{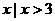 } C.{
} C.{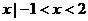 }
D. {
}
D. {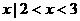 }
} 的部分图象是( )
的部分图象是( )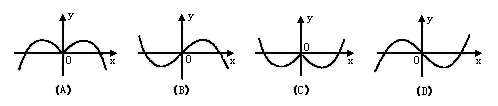
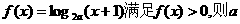 的取值范围是(
)
的取值范围是(
)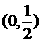 (B)
(B) (C)
(C)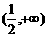 (D)
(D)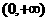
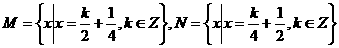 则( )
则( ) (B)
(B)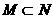 (C)
(C) (D)
(D)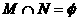
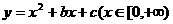 是单调函数的充要条件是( )
是单调函数的充要条件是( )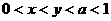 ,则有( )
,则有( )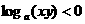 (B)
(B)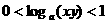
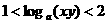 (D)
(D)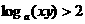
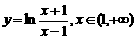 的反函数为( )
的反函数为( )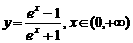 (B)
(B)
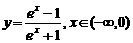 (D)
(D)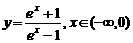
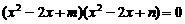 的四个根组成一个首项为
的四个根组成一个首项为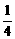 的等差数列,则
的等差数列,则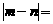 ( )
( )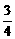 (C)
(C)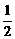 (D)
(D)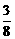
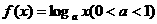 在区间
在区间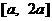 上的最大值是最小值的3倍,则a=(
)
上的最大值是最小值的3倍,则a=(
)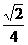 B.
B.
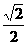 C.
C.
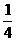 D.
D.
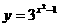 (
(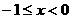 )的反函数是( )
)的反函数是( )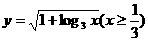 B.
B.
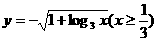
 D.
D.
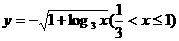
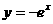 的图象( )
的图象( )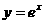 的图象关于y轴对称 B.与
的图象关于y轴对称 B.与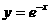 的图象关于
的图象关于 轴对称 D.与
轴对称 D.与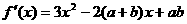 ,据题意知s,t为二次方程
,据题意知s,t为二次方程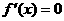 的两根…2分,
的两根…2分,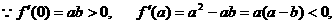
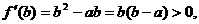
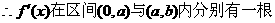 …6分
…6分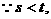
 …7分
…7分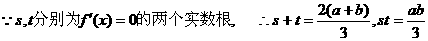 …9分
…9分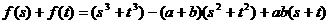
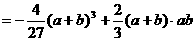
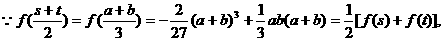
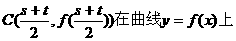 ………………………………14分
………………………………14分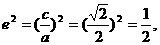 ∴
∴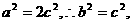 椭圆方程可设为:
椭圆方程可设为: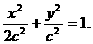 设直线l:y=k(x-1),显然k≠0,将直线方程代入椭圆方程:
设直线l:y=k(x-1),显然k≠0,将直线方程代入椭圆方程: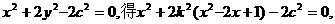 整理得:
整理得: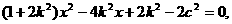 ①设交点A(
①设交点A(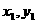 ),B(
),B(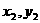 ),中点M(
),中点M(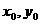 ),而中点在直线
),而中点在直线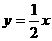 上, ∴
上, ∴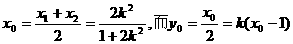
 ,求得:k=-1,将k=-1代入①,
,求得:k=-1,将k=-1代入①,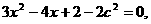
 ,点F(c,0)关于直线l:y=-x+1的对称点(1,1-c)在椭圆上,代入椭圆方程:∴1+2(1-c)2-2c2=0, ∴c=
,点F(c,0)关于直线l:y=-x+1的对称点(1,1-c)在椭圆上,代入椭圆方程:∴1+2(1-c)2-2c2=0, ∴c=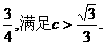 ∴所求椭圆为C:
∴所求椭圆为C: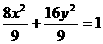 ,直线l方程为:
,直线l方程为: