0 446321 446329 446335 446339 446345 446347 446351 446357 446359 446365 446371 446375 446377 446381 446387 446389 446395 446399 446401 446405 446407 446411 446413 446415 446416 446417 446419 446420 446421 446423 446425 446429 446431 446435 446437 446441 446447 446449 446455 446459 446461 446465 446471 446477 446479 446485 446489 446491 446497 446501 446507 446515 447348
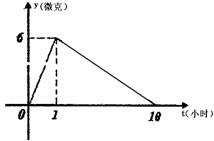
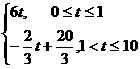
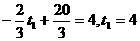 因而第二次服药应在11:00;
因而第二次服药应在11:00;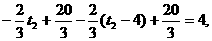 解得t2=9小时,故第三次服药应在16:00;
解得t2=9小时,故第三次服药应在16:00;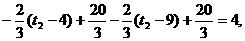 解得
解得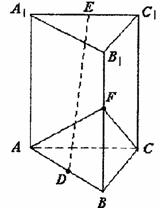 (1)求此三棱柱的高;
(1)求此三棱柱的高;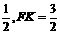 ,∴
,∴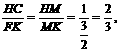
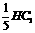 ,在Rt△HCC1,HC2=HM·HC1,
,在Rt△HCC1,HC2=HM·HC1,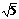 ,C1C=2.
,C1C=2.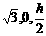 ),D(
),D( ),E(0,0,h),
),E(0,0,h),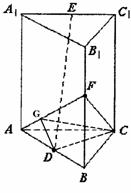 ∴
∴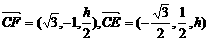 ,由CF⊥DE,得
,由CF⊥DE,得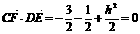 ,解得h=2.
,解得h=2.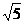 ,
,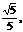 ∴tan∠CGD=
∴tan∠CGD=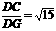 ,
,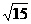 .
.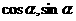 ),
),
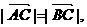 求角
求角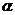 的值;
的值;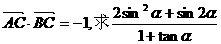 的值.
的值.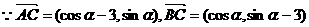
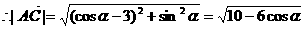 ,
,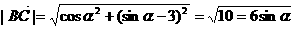 .
. 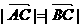 得
得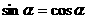 .
又
.
又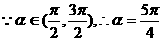 .(2)由
.(2)由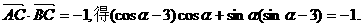
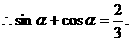 ①又
①又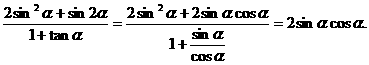 由①式两分平方得
由①式两分平方得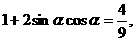
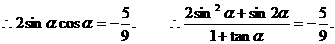
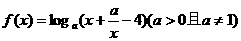 的值域是R,则实数a的取值范围
的值域是R,则实数a的取值范围
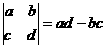 ,若复数
,若复数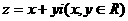 满足
满足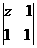 的模等于x,则复数z对应的Z(x,y)的轨迹方程为:
的模等于x,则复数z对应的Z(x,y)的轨迹方程为: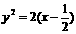 ;
;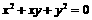 ,则代数式
,则代数式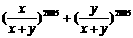 的值是1.
的值是1.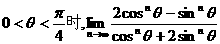 =2
=2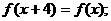 ②对于任意的
②对于任意的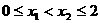 ,都有
,都有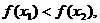 ③
③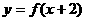 的图象关于y轴对称,则下列结论中,正确的是 (B)
的图象关于y轴对称,则下列结论中,正确的是 (B)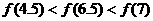 B.
B.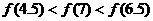
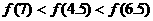 D.
D.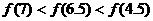
 将3种农作物都种植在如图的4块试验田里,每块种值一种
将3种农作物都种植在如图的4块试验田里,每块种值一种