24.本小题主要考查概率统计的基础知识,运用数学知识解决问题的能力.满分12分.
解:(Ⅰ)依题意,甲答对试题数ξ的概率分布如下:
|
ξ |
0 |
1 |
2 |
3 |
|
P |
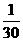 |
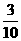 |
 |
 |
甲答对试题数ξ的数学期望
Eξ=0×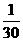 +1×
+1×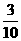 +2×
+2× +3×
+3× =
= .
.
(Ⅱ)设甲、乙两人考试合格的事件分别为A、B,则
P(A)= =
=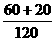 =
= ,
,
P(B)= =
= =
= .
.
因为事件A、B相互独立,
方法一:
∴甲、乙两人考试均不合格的概率为
P( )=P(
)=P( )P(
)P( )=1-
)=1- )(1-
)(1- )=
)= .
.
∴甲、乙两人至少有一人考试合格的概率为
P=1-P( )=1-
)=1- =
= .
.
答:甲、乙两人至少有一人考试合格的概率为 .
.
方法二:
∴甲、乙两人至少有一个考试合格的概率为
P=P(A· )+P(
)+P( ·B)+P(A·B)=P(A)P(
·B)+P(A·B)=P(A)P( )+P(
)+P( )P(B)+P(A)P(B)
)P(B)+P(A)P(B)
= ×
× +
+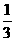 ×
× +
+ ×
× =
= .
.
答:甲、乙两人至少有一人考试合格的概率为 .
.
23.解:(Ⅰ)设A、B、C分别为甲、乙、丙三台机床各自加工的零件是一等品的事件.
|

由①、③得 代入②得 27[P(C)]2-51P(C)+22=0.
代入②得 27[P(C)]2-51P(C)+22=0.
解得
 (舍去).
(舍去).
将
 分别代入
③、② 可得
分别代入
③、② 可得 
即甲、乙、丙三台机床各加工的零件是一等品的概率分别是
(Ⅱ)记D为从甲、乙、丙加工的零件中各取一个检验,至少有一个一等品的事件,
则

故从甲、乙、丙加工的零件中各取一个检验,至少有一个一等品的概率为
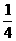 ,乙机床加工的零件是一等品而丙机床加工的零件不是一等品的概率为
,乙机床加工的零件是一等品而丙机床加工的零件不是一等品的概率为 ,甲、丙两台机床加工的零件都是一等品的概率为
,甲、丙两台机床加工的零件都是一等品的概率为 .
. . (结果用分数表示)
. (结果用分数表示) 的展开式中
的展开式中 的系数为
的系数为 ,则
,则 .-2
.-2 ___34 __行中从左至右第14与第15个数的比为
___34 __行中从左至右第14与第15个数的比为 .
. (结果用分数表示).
(结果用分数表示).