0 446307 446315 446321 446325 446331 446333 446337 446343 446345 446351 446357 446361 446363 446367 446373 446375 446381 446385 446387 446391 446393 446397 446399 446401 446402 446403 446405 446406 446407 446409 446411 446415 446417 446421 446423 446427 446433 446435 446441 446445 446447 446451 446457 446463 446465 446471 446475 446477 446483 446487 446493 446501 447348
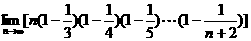 等于 ( )
等于 ( )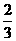 C.1 D.2
C.1 D.2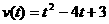 (米/秒)运动,则该质点在时刻
(米/秒)运动,则该质点在时刻 D.
D.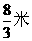
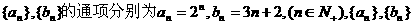 中相同项从小到大排成的新数列为{cn},则{cn}的第5项是 ( )
中相同项从小到大排成的新数列为{cn},则{cn}的第5项是 ( )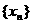 的前n项和为An,已知
的前n项和为An,已知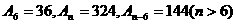 ,则n为( )
,则n为( )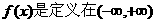 上的奇函数,且在区间(0,
上的奇函数,且在区间(0, )上单调递增,若
)上单调递增,若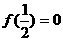 ,三角形的内角满足
,三角形的内角满足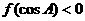 ,则A的取值范围是 ( )
,则A的取值范围是 ( )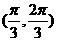 B.
B.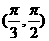
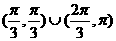 D.
D.
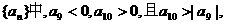 则在前n项和Sn中最大的负数为( )
则在前n项和Sn中最大的负数为( )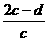 .
.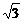 时,恒有f(x)>g(x).
时,恒有f(x)>g(x). (1)证明: y=f(x)=ax2+bx+c
(1)证明: y=f(x)=ax2+bx+c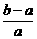 ,
,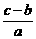 ,所以|A1B1|=|x1-x2|=
,所以|A1B1|=|x1-x2|=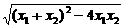
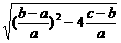 =
=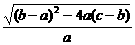 又a+b+c=0,故b=-(a+c)
又a+b+c=0,故b=-(a+c)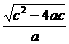 =
=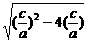 =
=
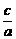 <-
<-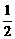 ∴|A1B1|的取值范围是(
∴|A1B1|的取值范围是(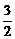 ,2
,2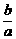 由a>b>c得:
由a>b>c得: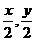 )
)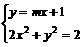 消去y得(2+m2)x2+2mx-1=0设A(x1,y1),B(x2,y2)
消去y得(2+m2)x2+2mx-1=0设A(x1,y1),B(x2,y2)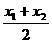 =-
=-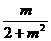 ,
,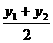 =m
=m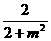
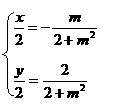
 于是
于是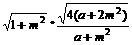
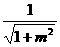 ·S(a)=|AB|d=
·S(a)=|AB|d=