0 446391 446399 446405 446409 446415 446417 446421 446427 446429 446435 446441 446445 446447 446451 446457 446459 446465 446469 446471 446475 446477 446481 446483 446485 446486 446487 446489 446490 446491 446493 446495 446499 446501 446505 446507 446511 446517 446519 446525 446529 446531 446535 446541 446547 446549 446555 446559 446561 446567 446571 446577 446585 447348
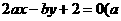 、b〉0)始终平分圆
、b〉0)始终平分圆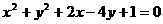 的周长,则
的周长,则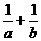 的最小值是( )
的最小值是( )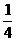 D.
D.
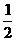
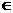 [
[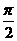 ,
,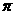 ],则y
],则y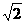 ]
]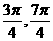 ]上是增函数
]上是增函数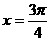 是函数图像的一条对称轴
是函数图像的一条对称轴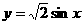 的图像向左平移
的图像向左平移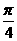 个单位得到
个单位得到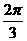 )到圆
)到圆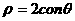 上动点的距离的最大值为( )
上动点的距离的最大值为( )  B.
B. C.2
D.1
C.2
D.1



 如图示,向放在水槽底部的烧杯注水(流量一定),
如图示,向放在水槽底部的烧杯注水(流量一定),













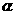 与L分别是一个平面和一条直线,则
与L分别是一个平面和一条直线,则 ”
” 是“A>15
是“A>15 ”的( )
”的( )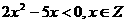 },若P∩Q≠
},若P∩Q≠ ,则m等于( )
,则m等于( )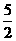 D. 1或2
D. 1或2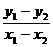 =x12+x22+x1x2-1
=x12+x22+x1x2-1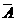 ,
,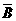 ,
,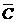 且P(A)=P(B)=P(C)=0.7,P(
且P(A)=P(B)=P(C)=0.7,P(