摘要:1.“x>-1 是“x>1 的( )
网址:http://m.1010jiajiao.com/timu3_id_4465013[举报]
已知函数f(x)=x2,对任意实数t,gt(x)=-tx+1.
(1)求函数y=g3(x)-f(x)的单调区间;
(2)h(x)=
-gt(x)在(0,2]上是单调递减的,求实数t的取值范围;
(3)若f(x)<mg2(x)对任意x∈(0,
]恒成立,求正数m的取值范围.
查看习题详情和答案>>
(1)求函数y=g3(x)-f(x)的单调区间;
(2)h(x)=
| x |
| f(x) |
(3)若f(x)<mg2(x)对任意x∈(0,
| 1 |
| 3 |
已知函数f(x)=x2,对任意实数t,gt(x)=-tx+1.
(1)求函数y=g3(x)-f(x)的单调区间;
(2)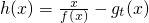 在(0,2]上是单调递减的,求实数t的取值范围;
在(0,2]上是单调递减的,求实数t的取值范围;
(3)若f(x)<mg2(x)对任意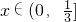 恒成立,求正数m的取值范围.
恒成立,求正数m的取值范围.
查看习题详情和答案>>
已知函数f(x)=x2,对任意实数t,gt(x)=-tx+1.
(1)求函数y=g3(x)-f(x)的单调区间;
(2) 在(0,2]上是单调递减的,求实数t的取值范围;
在(0,2]上是单调递减的,求实数t的取值范围;
(3)若f(x)<mg2(x)对任意 恒成立,求正数m的取值范围.
恒成立,求正数m的取值范围.
查看习题详情和答案>>
(1)求函数y=g3(x)-f(x)的单调区间;
(2)
 在(0,2]上是单调递减的,求实数t的取值范围;
在(0,2]上是单调递减的,求实数t的取值范围;(3)若f(x)<mg2(x)对任意
 恒成立,求正数m的取值范围.
恒成立,求正数m的取值范围.查看习题详情和答案>>
矩形ABCD的中心在坐标原点,边AB与x轴平行,AB=8,BC=6.E,F,G,H分别是矩形四条边的中点,R,S,T是线段OF的四等分点,R′,S′,T′是线段CF的四等分点.设直线ER与GR′,ES与GS′,ET与GT′的交点依次为L,M,N.
(1)求以HF为长轴,以EG为短轴的椭圆Q的方程;
(2)根据条件可判定点L,M,N都在(1)中的椭圆Q上,请以点L为例,给出证明(即证明点L在椭圆Q上).
(3)设线段OF的n(n∈N+,n≥2)等分点从左向右依次为Ri(i=1,2,…,n-1),线段CF的n等分点从上向下依次为Ti(i=1,2,…,n-1),那么直线ERi(i=1,2,…,n-1)与哪条直线的交点一定在椭圆Q上?(写出结果即可,此问不要求证明)

查看习题详情和答案>>
(1)求以HF为长轴,以EG为短轴的椭圆Q的方程;
(2)根据条件可判定点L,M,N都在(1)中的椭圆Q上,请以点L为例,给出证明(即证明点L在椭圆Q上).
(3)设线段OF的n(n∈N+,n≥2)等分点从左向右依次为Ri(i=1,2,…,n-1),线段CF的n等分点从上向下依次为Ti(i=1,2,…,n-1),那么直线ERi(i=1,2,…,n-1)与哪条直线的交点一定在椭圆Q上?(写出结果即可,此问不要求证明)
