0 446360 446368 446374 446378 446384 446386 446390 446396 446398 446404 446410 446414 446416 446420 446426 446428 446434 446438 446440 446444 446446 446450 446452 446454 446455 446456 446458 446459 446460 446462 446464 446468 446470 446474 446476 446480 446486 446488 446494 446498 446500 446504 446510 446516 446518 446524 446528 446530 446536 446540 446546 446554 447348
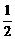 ,-
,-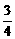 )
) =(4,3),向量
=(4,3),向量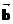 是垂直于
是垂直于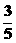 ,-
,-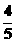 )或(-
)或(-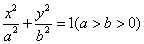 ,AA′是椭圆的长轴,P(x1,y1)是椭圆上异于A、A′的任意一点,过P点作斜率为
,AA′是椭圆的长轴,P(x1,y1)是椭圆上异于A、A′的任意一点,过P点作斜率为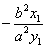 的直线l,若直线l上的两点M、M′在x轴上的射影分别为A、A′,则(1)|AM||A′M′|为定值b2;(2)由A、A′、M′、M四点构成的四边形面积的最小值为2ab.这一命题是真命题,证明如下:
的直线l,若直线l上的两点M、M′在x轴上的射影分别为A、A′,则(1)|AM||A′M′|为定值b2;(2)由A、A′、M′、M四点构成的四边形面积的最小值为2ab.这一命题是真命题,证明如下: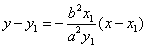 ,
,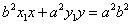 ,由射影的概念知M与A、M′与A′有相同的横坐标,
,由射影的概念知M与A、M′与A′有相同的横坐标,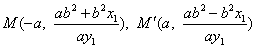 ,
,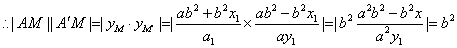 ;
;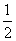 |AA′|(|AM|+|A′M′|),
|AA′|(|AM|+|A′M′|),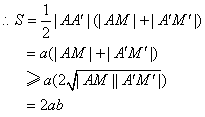
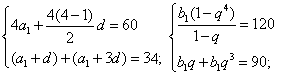
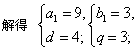 ∴ an=4n+5,bn=3n;
∴ an=4n+5,bn=3n;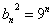 令4p+5=9n,得
令4p+5=9n,得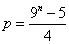 ,
,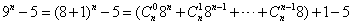 ,
,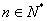 ,∴ 9n-5≥4,且上式小括号中的数为8的倍数,
,∴ 9n-5≥4,且上式小括号中的数为8的倍数,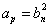 的正整数p总存在.
的正整数p总存在.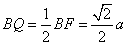 ,
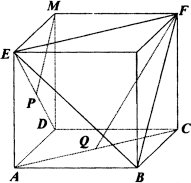
,
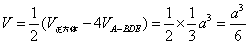 .
.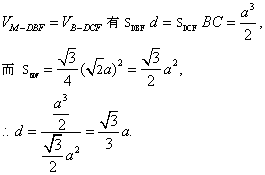
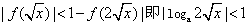 ,必有x>0,当0<x<1,
,必有x>0,当0<x<1,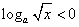 ,不等式化为
,不等式化为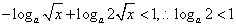 ,
,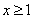 时,
时,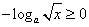 ,不等式化为
,不等式化为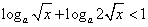 ,
,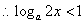 ,故
,故 ,此时
,此时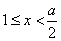 ;
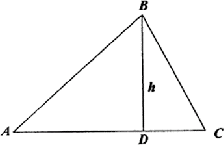
;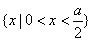 .
.
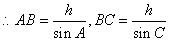 ,依题意得AB-BC=h,
,依题意得AB-BC=h, 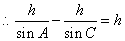 ,故得sinC-sinA=sinCsinA,
,故得sinC-sinA=sinCsinA,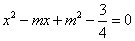 的两个根,
的两个根,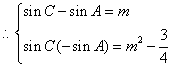 ;
;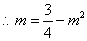 ,即
,即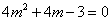 ,
,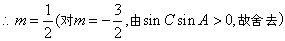 ,此时方程为
,此时方程为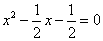 ,
,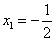 和x2=1,,∴ sinC=1,
和x2=1,,∴ sinC=1,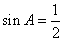 ,即有A=30°,C=90°.
,即有A=30°,C=90°.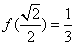 ,
,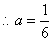 ,
,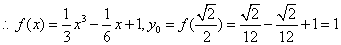 ,
,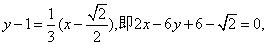
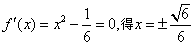 ,
,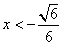 时,f′(x)>0,当
时,f′(x)>0,当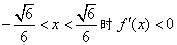 ,
,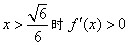 ,∴
函数f(x)有极大值
,∴
函数f(x)有极大值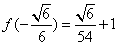 ,
,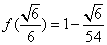 .
. 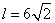 提示:由4a+2=2a-2,得a=-2, ∴平移后抛物线的焦点为F(-4,-6),
提示:由4a+2=2a-2,得a=-2, ∴平移后抛物线的焦点为F(-4,-6),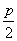 ,0)在y=x-2上,∴p=4, 由此可以求得平移公式为
,0)在y=x-2上,∴p=4, 由此可以求得平移公式为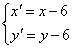 ,
, 提示:
提示: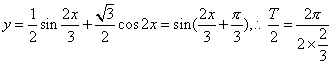 .
.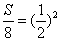 .
.