0 445989 445997 446003 446007 446013 446015 446019 446025 446027 446033 446039 446043 446045 446049 446055 446057 446063 446067 446069 446073 446075 446079 446081 446083 446084 446085 446087 446088 446089 446091 446093 446097 446099 446103 446105 446109 446115 446117 446123 446127 446129 446133 446139 446145 446147 446153 446157 446159 446165 446169 446175 446183 447348




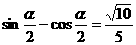 ,
, ,
,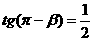 ,求tg(α-2β)的值。
,求tg(α-2β)的值。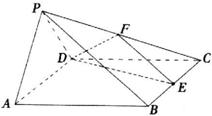
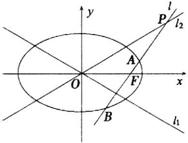
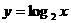 的图象交于
的图象交于 、
、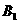 两点(
两点(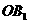 上,O为坐标原点),过
上,O为坐标原点),过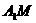 、
、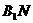 分别交函数
分别交函数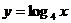 的图象于
的图象于 、
、 两点。
两点。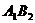 平行于x轴,求四边形
平行于x轴,求四边形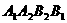 的面积。
的面积。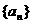 是由正数组成的等差数列,
是由正数组成的等差数列, 是其前n项的和,并且
是其前n项的和,并且 ,
, 。
。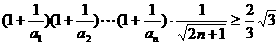 对一切n∈N均成立;
对一切n∈N均成立;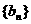 的通项公式满足
的通项公式满足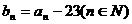 ,
,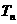 是其前n项的和,试问整数
是其前n项的和,试问整数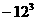 是否是数列
是否是数列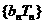 中的项?若是,则求出相应的项数;若不是,请说明理由。
中的项?若是,则求出相应的项数;若不是,请说明理由。 ,双曲线
,双曲线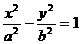 的两条渐近线为
的两条渐近线为 、
、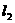 ,过椭圆C的右焦点F作直线l,使
,过椭圆C的右焦点F作直线l,使 ,又l与
,又l与 的最大值。
的最大值。