摘要:点P在双曲线=1上,F1.F2是左右焦点,O为原点, 求 的取值范围. 解: 设点P(x0,y0)在右支上,离心率为e, 则有|PF1|=ex0+a,|PF2|=ex0-a,|OP|==1, 所以, 设t=, ∴t2=,解得 这里t2-4>0,又≥a2, ∴≥a2 ∴≥1 ∴≥0,由此得: 解得2<t≤2e 当点P在左支上时,同理可以得出此结论.翰林汇翰林汇 翰林汇4.已知直线y=x+b与双曲线2x2-y2=2相交于A, B两点, 若以AB为直径的圆过原点, 求b的值翰林汇.翰林汇 解:翰林汇 设A(x1,y1), B(x2,y2), 则 由条件可得: x1+x2=2b, x1x2=-b2-2, y1y2=-x1x2, 最后得b=±2.翰林汇 翰林汇5.已知双曲线的中心在原点,对称轴为坐标轴,离心率,一条准线的方程为,求此双曲线的标准方程. 解: 由题设, 解得 . ∴双曲线方程为 .翰林汇
网址:http://m.1010jiajiao.com/timu3_id_4459971[举报]
设F1、F2是离心率为
的双曲线
-
=1(a>0,b>0)的左、右两个焦点,若双曲线右支上存在一点P,使(
+
)•
=0(O为坐标原点)且|PF1|=λ|PF2|则λ的值为( )
| 5 |
| x2 |
| a2 |
| y 2 |
| b2 |
| OP |
| OF2 |
| F2P |
| A、2 | ||
B、
| ||
| C、3 | ||
D、
|
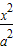 -
-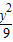 =1上,双曲线的一条渐近线为直线y=
=1上,双曲线的一条渐近线为直线y= x,左、右焦点分别是F1,F2.若PF1=5,则PF2的长为( )
x,左、右焦点分别是F1,F2.若PF1=5,则PF2的长为( ) -
- =1上,双曲线的一条渐近线为直线y=
=1上,双曲线的一条渐近线为直线y= x,左、右焦点分别是F1,F2.若PF1=5,则PF2的长为
x,左、右焦点分别是F1,F2.若PF1=5,则PF2的长为