0 445817 445825 445831 445835 445841 445843 445847 445853 445855 445861 445867 445871 445873 445877 445883 445885 445891 445895 445897 445901 445903 445907 445909 445911 445912 445913 445915 445916 445917 445919 445921 445925 445927 445931 445933 445937 445943 445945 445951 445955 445957 445961 445967 445973 445975 445981 445985 445987 445993 445997 446003 446011 447348
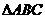 中,
中,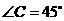 ,则
,则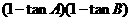 等于┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄(
)
等于┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄(
)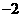 B.
B.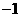 C.
C.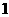 D.
D.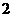
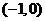 内的函数
内的函数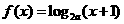 满足
满足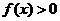 ,则实数
,则实数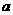 的取值范围为( )
的取值范围为( )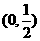 B.
B.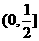 C.
C.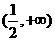 D.
D.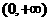
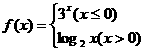 ,那么
,那么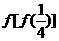 的值为┄┄┄┄┄┄┄┄┄┄┄┄┄┄( )
的值为┄┄┄┄┄┄┄┄┄┄┄┄┄┄( ) C.
C.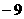 D.
D.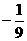
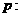
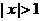 ,条件
,条件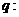
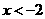 ,则
,则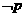 是
是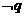 的┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄( )
的┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄( )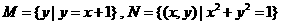 ,则集合
,则集合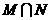 中元素的个数是┄┄( )
中元素的个数是┄┄( ) B.
B.
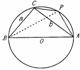
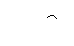 (I)求证:△ABC是直角三角形;(II)设圆O过A、B、C三点,点P位于劣弧AC上,∠PAB=60°,.求四边形ABCP的面积.
(I)求证:△ABC是直角三角形;(II)设圆O过A、B、C三点,点P位于劣弧AC上,∠PAB=60°,.求四边形ABCP的面积. 解:(Ⅰ)证明:根据正弦定理得,
解:(Ⅰ)证明:根据正弦定理得,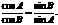
 整理为,sinAcosA=sinBcosB,即sin2A=sin2B.
整理为,sinAcosA=sinBcosB,即sin2A=sin2B. 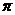 ∴
∴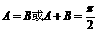 .
.
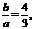 ∴舍去A=B. ∴
∴舍去A=B. ∴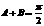 即
即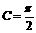 .故△ABC是直角三角形.
.故△ABC是直角三角形.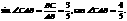
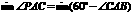 =
=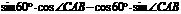 =
=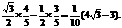
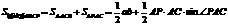 =24+
=24+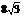
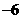 =18+
=18+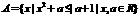 .(1)求
.(1)求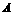 ;(2)若以
;(2)若以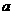 为首项,
为首项,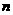 项和记为
项和记为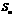 ,对于任意的
,对于任意的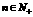 ,均有
,均有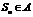 ,求
,求 得
得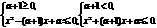
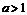 时,
时,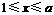 .当
.当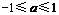 时,
时, 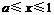 ,当
,当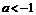 时,
时,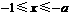 .综上,
.综上, 时,
时, ;
;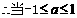 时,
时,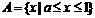 ;当
;当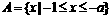 .
.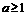 时,
时, ,故
,故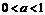 时,
时, ,而
,而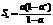 是关于
是关于 且无限接近
且无限接近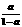 时,对任意的
时,对任意的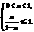 解得
解得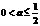 . 当
. 当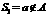 ,故不存在实数
,故不存在实数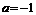 时,
时,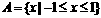 .
.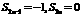 ,适合.当
,适合.当 时,
时, .
.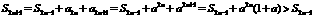 ,
,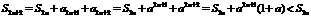 ,
, ,且
,且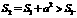 故
故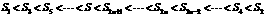 .
.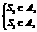 即
即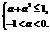 解得
解得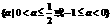 .
. 的直线交y=x(x>0)于点Q,动点M在什么位置时,
的直线交y=x(x>0)于点Q,动点M在什么位置时,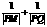 有最大值,并求出这个最大值.
有最大值,并求出这个最大值.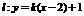 ,要它与
,要它与 相交,则
相交,则 .
. ,令
,令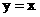 ,得
,得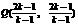 . ∴
. ∴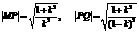 .
.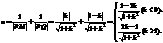 于是
于是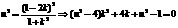 .由
.由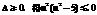 ,∴
,∴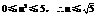 .而当l的方程为x=2时,u=2,
∴
.而当l的方程为x=2时,u=2,
∴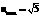 对应得k=-2,
对应得k=-2, 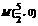 .
.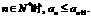 (Ⅰ)请给出一个具有这种性质的无穷数列,使得不等式
(Ⅰ)请给出一个具有这种性质的无穷数列,使得不等式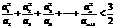 对于任意的
对于任意的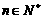 都成立,并对你给出的结果进行验证(或证明);(Ⅱ)若
都成立,并对你给出的结果进行验证(或证明);(Ⅱ)若 ,其中
,其中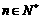 ,且记数列{bn}的前n项和Bn,证明:
,且记数列{bn}的前n项和Bn,证明: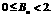
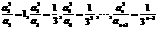 ,则无穷数列{an}可由a1
= 1,
,则无穷数列{an}可由a1
= 1,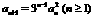 给出.
给出.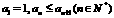 ,且
,且
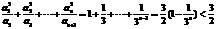
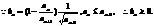
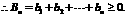 又
又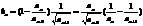
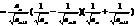
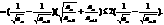
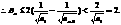
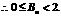
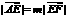 (
(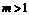 ),
),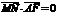 ,
,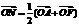 ,
,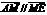 .(Ⅰ)求点M的轨迹W的方程;(Ⅱ)点
.(Ⅰ)求点M的轨迹W的方程;(Ⅱ)点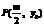 在轨迹W上,直线PF交轨迹W于点Q,且
在轨迹W上,直线PF交轨迹W于点Q,且 ,若
,若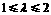 ,求实数
,求实数 的范围.
的范围.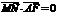 ,
,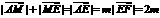 ,
,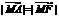 ,∴
,∴ 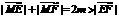 , ∴ 点M的轨迹W是以E、F为焦点的椭圆,且半长轴
, ∴ 点M的轨迹W是以E、F为焦点的椭圆,且半长轴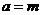 ,半焦距
,半焦距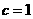 ,∴
,∴ 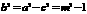 .
.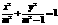 (
(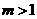 ).
).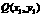 ∵
∵ 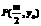 ,
,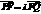 ,∴
,∴ 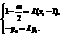 ∴
∴ 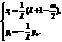
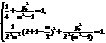 消去
消去 并整理,得
并整理,得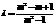 ,由
,由 及
及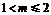 .
. 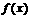 的定义域为
的定义域为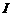 ,导数
,导数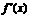 满足0<
满足0<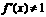 ,常数
,常数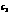 为方程
为方程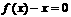 的实数根,常数
的实数根,常数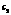 为方程
为方程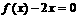 的实数根.(Ⅰ)若对任意
的实数根.(Ⅰ)若对任意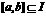 ,存在
,存在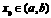 ,使等式
,使等式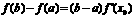 成立.试问:方程
成立.试问:方程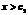 时,总有
时,总有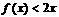 成立;(Ⅲ)对任意
成立;(Ⅲ)对任意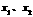 ,若满足
,若满足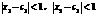 ,求证:
,求证: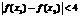 。
。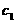 的实根m,即
的实根m,即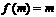 .则有
.则有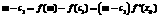 成立
.因为
成立
.因为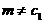 ,所以必有
,所以必有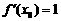 ,但这与
,但这与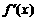 ≠1矛盾,因此方程
≠1矛盾,因此方程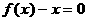 不存在异于c1的实数根.∴方程
不存在异于c1的实数根.∴方程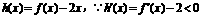 ,∴函数
,∴函数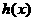 为减函数.又
为减函数.又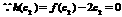 ,
,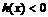 ,即
,即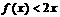 成立.
成立.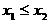 ,
,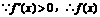 为增函数,即
为增函数,即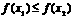 .又
.又 ,∴函数
,∴函数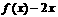 为减函数即
为减函数即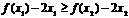 .
.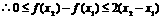 ,即
,即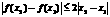 .
.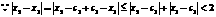 ,
,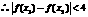 .
. ,bn=
,bn=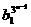 ,
,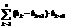
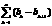 =b1-bn+1<b1<1。
=b1-bn+1<b1<1。
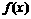 满足:f(0) = 2,f(1) = 3,且
满足:f(0) = 2,f(1) = 3,且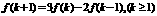 .
.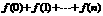 .
.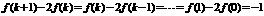 ,所以有:
,所以有: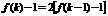 ,又
,又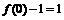 ,所以
,所以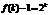 ,即
,即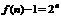 故
故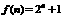 .
.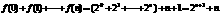 .
.