0 445841 445849 445855 445859 445865 445867 445871 445877 445879 445885 445891 445895 445897 445901 445907 445909 445915 445919 445921 445925 445927 445931 445933 445935 445936 445937 445939 445940 445941 445943 445945 445949 445951 445955 445957 445961 445967 445969 445975 445979 445981 445985 445991 445997 445999 446005 446009 446011 446017 446021 446027 446035 447348
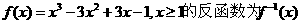 ,则下列结论正确的是( )
,则下列结论正确的是( )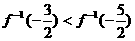 B.
B.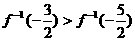
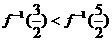 D.
D.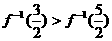
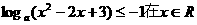 上恒成立,则实数a的取值范围是 ( )
上恒成立,则实数a的取值范围是 ( )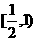 B.(1,2
B.(1,2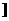 C.
C.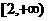 D.
D.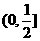
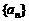 中,已知
中,已知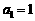 ,
,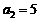 ,
,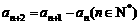 ,则
,则 ( )
( ) B.5 C.
B.5 C.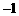 D.1
D.1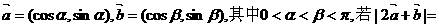
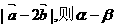 等于 ( )
等于 ( )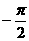 B.
B.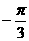 C.
C.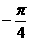 D.
D.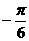
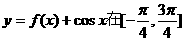 内单调递减,则f(x)可以是 ( )
内单调递减,则f(x)可以是 ( )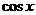 C.
C.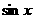 D.
D.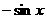
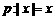 ,条件
,条件 ,则p是q的 ( )
,则p是q的 ( )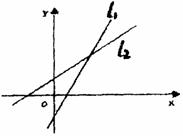 4.已知直线方程分别为l1:
4.已知直线方程分别为l1: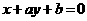 ,l2:
,l2: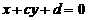 ,它们在直角坐标系中的位置如图,则 ( )
,它们在直角坐标系中的位置如图,则 ( )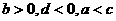
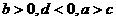
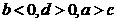
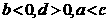
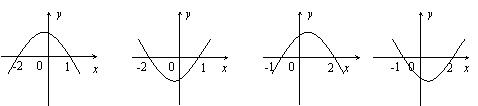 不等式
不等式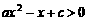 的解集为
的解集为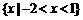 ,则函数
,则函数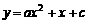 的图象大致为( )
的图象大致为( )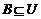 ,若
,若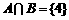 ,
,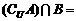 {2, 5},则B=( )
{2, 5},则B=( ) (本题满分12分)
(本题满分12分)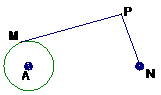 过动点P作A的切线PM(M为切点),连结PN使得PM:PN=
过动点P作A的切线PM(M为切点),连结PN使得PM:PN=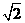 ,试建立适当的坐标系,求动点P的轨迹
,试建立适当的坐标系,求动点P的轨迹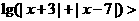 a
a
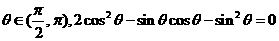 ,求
,求 和
和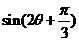 的值
的值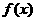 的二次项系数为
的二次项系数为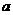 ,且不等式
,且不等式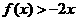 的解集为
的解集为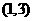
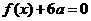 有两个相等的实数根,求
有两个相等的实数根,求 的无极值,求实数
的无极值,求实数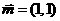 ,向量
,向量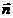 与向量
与向量 的夹角为
的夹角为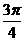 ,且
,且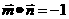

 的夹角为
的夹角为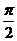 ,向量
,向量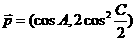 ,其中A,C为△ABC的内角,且B=600,求
,其中A,C为△ABC的内角,且B=600,求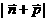 的取值范围
的取值范围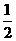 (3n+Sn)对一切正整数n成立
(3n+Sn)对一切正整数n成立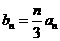 ,求数列
,求数列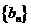 的前n项和Bn;
的前n项和Bn;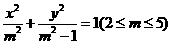
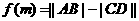
 的解析式;
的解析式;