摘要:(三)存在性探索型 例3 已知抛物线y=(1-m)x2+4x-3开口向下.与x轴交于A(x1.0)和B(x2.0)两点.其中x1<x2. (1)求m的取值范围, (2)若两根的平方和为10.求抛物线的解析式.并在给出直角坐标系中画出这条抛物线, (3)设这条抛物线的顶点为C.延长CA交y轴于点D.在y轴上是否存在点P.使以P.O.B为顶点的三角形与△BCD相似?若存在.求出P点的坐标,若不存在.请说明理由. 分析:(1)易求1<m<,(2)易求解析式为y=-x2+4x-3, (3)假设Rt△POB与Rt△BCD相似.则=或=.解得PO=或PO=6.符合题意.∴点P的坐标为.. 例4 如图.梯形OABC中.O为直角坐标系的原点.A.B.C的坐标分别为. 点P.Q同时从原点出发.分别作匀速运动.其中点P沿OA向终点A运动.速度为每秒1个单位,点Q沿OC.CB向终点B运动.当这两点中有一点到达自己的终点时.另一点也停止运动. (1)设从出发起运动了x秒.如果点Q的速度为每秒2个单位.试分别写出这时点Q在OC上或在CB上时的坐标(用含x的代数式表示.不要求写出x的取值范围): (2)设从出发起运动了x秒.如果点P与点Q所经过的路程之和恰好为梯形OABC的周长的一半. ①试用含x的代数式表示这时点Q所经过的路程和它的速度, ②试问:当点Q在OC上时.直线PQ是否可能同时把梯形OABC的面积也分成相等的两部分?如有可能.求出相应的x的值和P.Q的坐标,如不能.请说明理由. 图3 图4 分析:(1)当点Q在OC上时.坐标为(x.x).当点Q在CB上.坐标为. (2)①点Q所经过的路程为16-x.速度为.②当Q在OC上时.作QM⊥OA.垂足为M.则QM=×.∴S△OPQ=וx=×.令x=18.解之.得x1=10.x2=6.∵当x1=10时.16-x=6,这时点Q不在OC上.故舍去.当x2=6.16-x=10.这时点Q不在OC上.故舍去. ∴当Q点在OC上时.PQ不可能同时把梯形OABC的面积也分成相等的两部分. 评析:这例题的特征是探索命题的结论或结论的某些方面是否存在.解题思路是:假设存在--演绎推理--得出结论.若结论合理.则存在,若结论不合理.产生矛盾.则不存在.
网址:http://m.1010jiajiao.com/timu3_id_440813[举报]
阅读探索:“任意给定一个矩形A,是否存在另一个矩形B,它的周长和面积分别是已知矩形周长和面积的一半?”(完成下列空格)
(1)当已知矩形A的边长分别为6和1时,小亮同学是这样研究的:
设所求矩形的两边分别是x和y,由题意得方程组: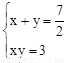 ,
,
∵△=49-48>0,∴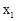 =
,
=
,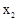 =
.
=
.
∴满足要求的矩形B存在.
(2)如果已知矩形A的边长分别为2和1,请你仿照小亮的方法研究是否存在满足要求的矩形B.
(3)如果矩形A的边长为m和n,请你研究满足什么条件时,矩形B存在?
查看习题详情和答案>>
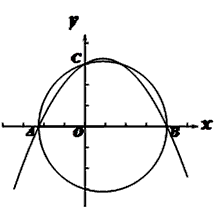
如图所示,在平面直角坐标系O中xy,已知点A(- ,0),点C(0,3),点B是x轴上一点(位于点A的右侧),以AB为直径的圆恰好经过点C。
,0),点C(0,3),点B是x轴上一点(位于点A的右侧),以AB为直径的圆恰好经过点C。
(1)求∠ACB的度数;
(2)已知抛物线线y=ax2+bx+3过A、B两点,求抛物线的解析式;
(3)线段BC上是否存在点D,使△BOD为等腰三角形,若存在,则求出所有符合条件的点D的坐标;若不存在,请说明理由。
 ,0),点C(0,3),点B是x轴上一点(位于点A的右侧),以AB为直径的圆恰好经过点C。
,0),点C(0,3),点B是x轴上一点(位于点A的右侧),以AB为直径的圆恰好经过点C。(1)求∠ACB的度数;
(2)已知抛物线线y=ax2+bx+3过A、B两点,求抛物线的解析式;
(3)线段BC上是否存在点D,使△BOD为等腰三角形,若存在,则求出所有符合条件的点D的坐标;若不存在,请说明理由。
已知抛物线y=ax2+4ax+t与x轴的一个交点为A(-1,0).
(1)求抛物线与x轴的另一个交点B的坐标;
(2)D是抛物线与y轴的交点,C是抛物线上的一点,且以AB为一底的梯形ABCD的面积为9,求此抛物线的解析式;
(3)E是第二象限内到x轴、y轴的距离的比为5:2的点,如果点E在(2)中的抛物线上,且它与点A在此抛物线对称轴的同侧,问:在抛物线的对称轴上是否存在点P,使ΔAPE的周长最小?若存在,求出点P的坐标;若不存在,请说明理由.
查看习题详情和答案>>
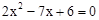 ,
,