(二)结论探索型例2:如图1.AB是⊙O的直径.AC是弦.直线CD切⊙O于点C.AD⊥CD.垂足为D. (1)求证:AC2＝AB·AD, (2)若将直线CD向上平移.交⊙O于点C1.C2两点.——青夏教育精英家教网——

摘要：(二)结论探索型例2:如图1.AB是⊙O的直径.AC是弦.直线CD切⊙O于点C.AD⊥CD.垂足为D. (1)求证:AC2＝AB·AD, (2)若将直线CD向上平移.交⊙O于点C1.C2两点.其它条件不变.可得到图2所示的图形.试探索AC1.AC2.AB.AD之间的关系.并说明理由．图1 图2 分析:(1)连结BC.可证△ACD∽△ABC．(2)关系:AC1·AC2＝AB·AD.可证△ADC2∽△AC1B．评析:这类题的特征是给定条件.但结论不确定.其解题一般思路为:已知条件――演绎推理--推出结论．若是遇到与自然数有关的问题.则可采用归纳――猜想――证明的思维方法.去探求结论．

网址：http://m.1010jiajiao.com/timu3_id_440812[举报]

阅读理解：
对于任意正实数a，b，∵(

)2≥0，∴a-2

+b≥0，∴a+b≥2

，只有点a=b时，等号成立．
结论：在a+b≥2

（a，b均为正实数）中，若ab为定值p，则a+b≥2

，只有当a=b时，a+b有最小值2

．
根据上述内容，回答下列问题：
（1）若m＞0，只有当m=

；
（2）思考验证：
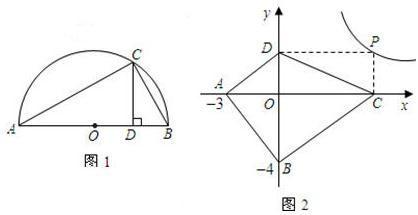
①如图1，AB为半圆O的直径，C为半圆上任意一点，（与点A，B不重合）．过点C作CD⊥AB，垂足为D，AD=a，DB=b．试根据图形验证a+b≥2

，并指出等号成立时的条件；
②探索应用：如图2，已知A（-3，0），B（0，-4）P为双曲线y=

(x＞0)上的任意一点，过点P作PC⊥x轴于点C，PD⊥y轴于点D．求四边形ABCD面积的最小值，并说明此时四边形ABCD的形状．

查看习题详情和答案>>

阅读理解：
对于任意正实数a，b，因为(

)2≥0，所以a-2

+b≥0，所以a+b≥2

，只有当a=b时，等号成立．
结论：在a+b≥2

（a，b均为正实数）中，若ab为定值p，则a+b≥2

，只有当a=b时，a+b有最小值2

．
（1）根据上述内容，回答下列问题：若m＞0，只有当m=

；
（2）探索应用：如图，有一均匀的栏杆，一端固定在A点，在离A端2米的B处垂直挂着一个质量为8千克的重物．若已知每米栏杆的质量为0.5千克，现在栏杆的另一端C用一个竖直向上的拉力F拉住栏杆，使栏杆水平平衡．试

问栏杆多少长时，所用拉力F最小？是多少？查看习题详情和答案>>

阅读理解：
对于任意正实数a、b，∵(

)2≥0，∴a-2

+b≥0，
∴a+b≥2

，只有当a=b时，等号成立．
结论：在a+b≥2

（a、b均为正实数）中，若ab为定值p，则a+b≥2

，只有当a=b时，a+b有最小值2

．
（1）根据上述内容，回答下列问题：
若m＞0，只有当m=

．
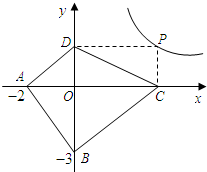
（2）探索应用：如图，已知A（-3，0），B（0，-4），P为双曲线y=

（x＞0）图象上的任意一点，过点P作PC⊥x轴于点C，PD⊥y轴于点D．求四边形ABCD面积的最小值．
（3）判断此时四边形ABCD的形状，说明理由．

查看习题详情和答案>>

阅读理解：对于任意正实数a，b，
∵（

）²≥0，
∴a-2

+b≥0，
∴a+b≥2

，只有当a=b时，等号成立．
结论：在a+b≥2

（a，b均为正实数）中，若ab为定值P，则a+b≥2

，
当a=b，a+b有最小值2

．
根据上述内容，回答下列问题：
（1）若x＞0，x+

的最小值为

．
（2）探索应用：如图，已知A（-2，0），B（0，-3），点P为双曲线y=

（x＞0）上的任意一点，过点P作PC⊥x轴于点C，PD⊥y轴于点D．求四边形ABCD面积的最小值，并说明此时四边形ABCD的形状．查看习题详情和答案>>

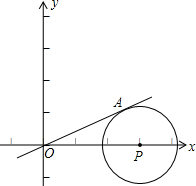我们知道两个一次函数y=k₁x+b₁，y=k₂x+b₂，当k₁=k₂时，这两个一次函数的图象相互平行，那么两个一次函数的图象什么情况下相互垂直呢？下面我们就来探索．
（1）画一画
在同一平面直角坐标系下画出一次函数y=2x+1，y=-2x+3，y=

x+2的图象；
（2）想一想
仔细观察图象，结合四个一次函数的解析式提出猜想：当

时，两个一次函数y=k₁x+b₁，y=k₂x+b₂的图象相互垂直；
（3）用一用
利用（2）中的结论解决下面问题如图：已知正比例函数y=

x的图象和⊙P相切于点A，点P在x轴上，OP=3厘米，求⊙P的面积．

查看习题详情和答案>>