20.(2011湖北鄂州,20,8分)今年我省干旱灾情严重,甲地急需要抗旱用水15万吨,乙地13万吨.现有A、B两水库各调出14万吨水支援甲、乙两地抗旱.从A地到甲地50千米,到乙地30千米;从B地到甲地60千米,到乙地45千米.
⑴设从A水库调往甲地的水量为x万吨,完成下表


|
甲 |
乙 |
总计 |
||||||
|
A |
x |
|
14 |
||||||
|
B |
|
|
14 |
||||||
|
总计 |
15 |
13 |
28 |
⑵请设计一个调运方案,使水的调运量尽可能小.(调运量=调运水的重量×调运的距离,单位:万吨•千米)
[解题思路]通过读题、审题
(1)完成表格有2个思路:从供或需的角度考虑,均能完成上表。
(2)运用公式(调运水的重量×调运的距离)
总调运量=A的总调运量+B的总调运量调运水的重量×调运的距离
y=50x+(14-x)30+60(15-x)+(x-1)45=5x+1275(注:一次函数的最值要得到自变量的取值范围)∵5>0∴y随x的增大而增大,y要最小则x应最大
由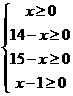 解得1≤x≤14
解得1≤x≤14
y=5x+1275中∵5>0∴y随x的增大而增大,y要最小则x应最小=1
∴调运方案为A往甲调1吨,往乙调13吨;B往甲调14吨,不往乙调。
[答案]⑴(从左至右,从上至下)14-x 15-x x-1
⑵y=50x+(14-x)30+60(15-x)+(x-1)45=5x+1275
解不等式1≤x≤14
所以x=1时y取得最小值
y=5+1275=1280
∴调运方案为A往甲调1吨,往乙调13吨;B往甲调14吨,不往乙调。
[点评]这样的“方案决策类”试题,其所考查的内容和思想方法却是非常重要的,其考查目的也是一般的函数与不等式题目所不能完全体现的,具有一定的独特性和挑战性.在多数情况下,解这种试题要以“不等式” 作为解决问题的工具,且由于题中含有由“不确定”中找确定的因素,所以关联了函数与不等式等数学模型的建立与应用。此题中要确定一个量的范围的问题,就要转化为不等式的问题.
上题对于学生来说问题情境还是比较熟悉的,且题目中都是显性的条件,学生通过认真审题能比较容易将实际问题转化为数学问题,从而求解。第(2)问需要借助题目中隐含的不等关系--难点,列出不等式组,并确定出不等数组的解,从而利用一次函数的增减性选择最值,得到最佳方案。
难度较大
19.(2011湖北鄂州,19,7分)有3张扑克牌,分别是红桃3、红桃4和黑桃5.把牌洗匀后甲先抽取一张,记下花色和数字后将牌放回,洗匀后乙再抽取一张.
⑴先后两次抽得的数字分别记为s和t,则︱s-t︱≥1的概率.
⑵甲、乙两人做游戏,现有两种方案.A方案:若两次抽得相同花色则甲胜,否则乙胜.B方案:若两次抽得数字和为奇数则甲胜,否则乙胜.
请问甲选择哪种方案胜率更高?
[解题思路](1)如下表
|
甲(s) 乙(t) |
红桃3 |
红桃4 |
黑桃5 |
|
红桃3 |
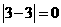 |
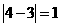 |
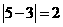 |
|
红桃4 |
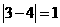 |
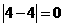 |
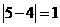 |
|
黑桃5 |
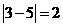 |
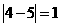 |
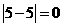 |
由上表可知:︱s-t︱≥1的概率=
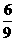 =
= (也可画树形图求解)。
(也可画树形图求解)。
(2)方案A:如表
|
甲(花色) 乙(花色) |
红桃3 |
红桃4 |
黑桃5 |
|
红桃3 |
同色 |
同色 |
不同色 |
|
红桃4 |
同色 |
同色 |
不同色 |
|
黑桃5 |
不同色 |
不同色 |
同色 |
由上表可得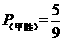
方案B:如表
|
甲 乙 |
红桃3 |
红桃4 |
黑桃5 |
|
红桃3 |
3+3=6 |
3+4=7 |
3+5=8 |
|
红桃4 |
4+3=7 |
4+4=8 |
4+5=9 |
|
黑桃5 |
5+3=8 |
5+4=9 |
5+5=10 |
由上表可得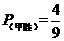
因为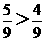 ,所以选择A方案甲的胜率更高.
,所以选择A方案甲的胜率更高.
[答案]⑴ ⑵A方案
⑵A方案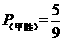 ,B方案
,B方案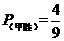 ,故选择A方案甲的胜率更高.
,故选择A方案甲的胜率更高.
[点评]本题考查的是用列表法或画树状图法求概率方法.列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,列表适合于两步完成的事件.用到的知识点为:概率=所求情况数与总情况数之比.
难度中等


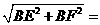 5
5

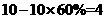 瓶,所以优秀率为
瓶,所以优秀率为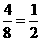
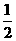
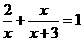
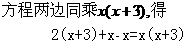
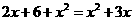
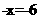
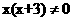 ,所以x=6是原方程的根。
,所以x=6是原方程的根。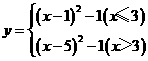 ,则使y=k成立的x值恰好有三个,则k的值为( )
,则使y=k成立的x值恰好有三个,则k的值为( )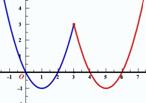
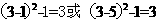 ,则k的值为3。
,则k的值为3。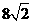
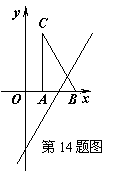

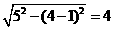 ,所以平行四边形面积=底×高=4×4=16.
,所以平行四边形面积=底×高=4×4=16.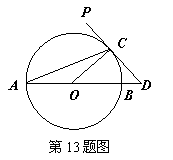

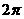 B.
B.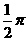 C.
C. 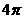 D.
D.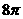


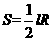 =
= 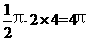
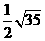
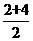 =3,众数为2,命题正确;③等腰梯形只是轴对称图形,不是中心对称图形,命题不正确;
=3,众数为2,命题正确;③等腰梯形只是轴对称图形,不是中心对称图形,命题不正确;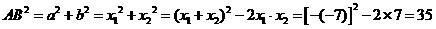 ,
,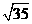 ,而斜边上的中线等于斜边的一半为
,而斜边上的中线等于斜边的一半为