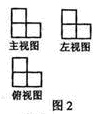
0 43490 43498 43504 43508 43514 43516 43520 43526 43528 43534 43540 43544 43546 43550 43556 43558 43564 43568 43570 43574 43576 43580 43582 43584 43585 43586 43588 43589 43590 43592 43594 43598 43600 43604 43606 43610 43616 43618 43624 43628 43630 43634 43640 43646 43648 43654 43658 43660 43666 43670 43676 43684 447348
 C.到一条绕段两端点距离相等的点在该线段的垂直平分线上
C.到一条绕段两端点距离相等的点在该线段的垂直平分线上
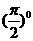 是无理数 B.
是无理数 B.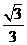 是有理数 C.
是有理数 C.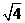 是无理数 D.
是无理数 D.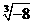 是有理数
是有理数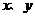 为实数,且
为实数,且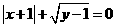 ,则
,则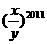 的值是
的值是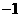 D.
D.
 A.
A.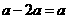 B.
B.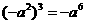 C.
C.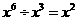 D.
D.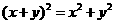
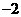 的倒数是
的倒数是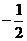 D.
D.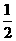
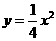 交于M(x1,y1)和N(x2,y2)两点(其中x1<0,x2<0).
交于M(x1,y1)和N(x2,y2)两点(其中x1<0,x2<0).

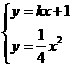 变形得关于x的一元二次方程,
变形得关于x的一元二次方程,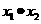 =-4
=-4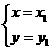 和
和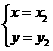 是方程组
是方程组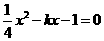 ,依据“根与系数关系”得
,依据“根与系数关系”得
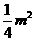 ,计算知NN1=
,计算知NN1=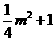 , NF=
, NF=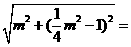
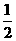 (MM1+NN1)=
(MM1+NN1)=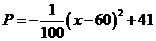 (万元).当地政府拟在“十二•五”规划中加快开发该特产的销售,其规划方案为:在规划前后对该项目每年最多可投入100万元的销售投资,在实施规划5年的前两年中,每年都从100万元中拨出50万元用于修建一条公路,两年修成,通车前该特产只能在当地销售;公路通车后的3年中,该特产既在本地销售,也在外地销售.在外地销售的投资收益为:每投入x万元,可获利润
(万元).当地政府拟在“十二•五”规划中加快开发该特产的销售,其规划方案为:在规划前后对该项目每年最多可投入100万元的销售投资,在实施规划5年的前两年中,每年都从100万元中拨出50万元用于修建一条公路,两年修成,通车前该特产只能在当地销售;公路通车后的3年中,该特产既在本地销售,也在外地销售.在外地销售的投资收益为:每投入x万元,可获利润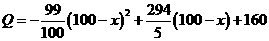 (万元)
(万元)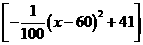 +
+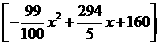 =
=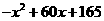 =
=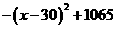 ,表明x=30时,y最大且为1065,那么三年获利最大为1065×3=3495万元,
,表明x=30时,y最大且为1065,那么三年获利最大为1065×3=3495万元,

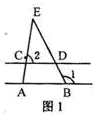
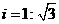 (指坡面的铅直高度与水平宽度的比).且AB=20 m.身高为1.7 m的小明站在大堤A点,测得高压电线杆端点D的仰角为30°.已知地面CB宽30
m,求高压电线杆CD的高度(结果保留三个有效数字,
(指坡面的铅直高度与水平宽度的比).且AB=20 m.身高为1.7 m的小明站在大堤A点,测得高压电线杆端点D的仰角为30°.已知地面CB宽30
m,求高压电线杆CD的高度(结果保留三个有效数字,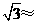 1.732).
1.732).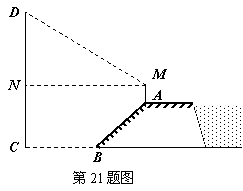


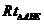 中,背水坡AB的坡比
中,背水坡AB的坡比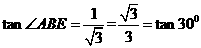 ,
,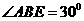 。又AB=20 m,所以AE=
。又AB=20 m,所以AE= 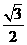 =
= 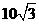 m
m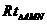 中,∠AMN=30°,MN=CE=CB+BE=(30+
中,∠AMN=30°,MN=CE=CB+BE=(30+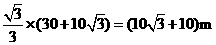
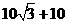 =
= 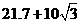 ≈36.0m
≈36.0m