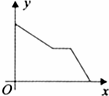
0 43476 43484 43490 43494 43500 43502 43506 43512 43514 43520 43526 43530 43532 43536 43542 43544 43550 43554 43556 43560 43562 43566 43568 43570 43571 43572 43574 43575 43576 43578 43580 43584 43586 43590 43592 43596 43602 43604 43610 43614 43616 43620 43626 43632 43634 43640 43644 43646 43652 43656 43662 43670 447348
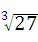 +
+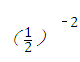 .
. ,
,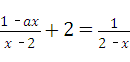 有正整数解的概率为
有正整数解的概率为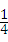 .
.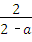 ,
, 的圆中,45°的圆心角所对的弧长等于 1 .
的圆中,45°的圆心角所对的弧长等于 1 .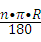 把半径和圆心角代入进行计算即可.
把半径和圆心角代入进行计算即可. =1.
=1.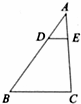
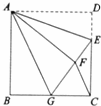
 CD=2,设BG=FG=x,则CG=6﹣x.在直角△ECG中,根据勾股定理,得(6﹣x)2+42=(x+2)2,解得x=3.所以BG=3=6﹣3=GC;
CD=2,设BG=FG=x,则CG=6﹣x.在直角△ECG中,根据勾股定理,得(6﹣x)2+42=(x+2)2,解得x=3.所以BG=3=6﹣3=GC;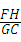 =
=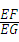 ,
,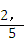 ,
, ×3×4﹣
×3×4﹣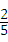 ×3)=
×3)=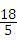 ≠3.
≠3.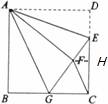
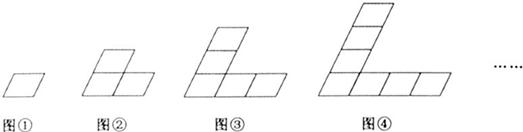
 B、
B、
 D、
D、