25、(2011•潼南县)潼南绿色无公害蔬菜基地有甲、乙两种植户,他们种植了A、B两类蔬菜,两种植户种植的两类蔬菜的种植面积与总收入如下表:
|
种植户 |
种植A类蔬菜面积 (单位:亩) |
种植B类蔬菜面积 (单位:亩) |
总收入 (单位:元) |
|
甲 |
3 |
1 |
12500 |
|
乙 |
2 |
3 |
16500 |
说明:不同种植户种植的同类蔬菜每亩平均收入相等.
(1)求A、B两类蔬菜每亩平均收入各是多少元?
(2)某种植户准备租20亩地用来种植A、B两类蔬菜,为了使总收入不低于63000元,且种植A类蔬菜的面积多于种植B类蔬菜的面积(两类蔬菜的种植面积均为整数),求该种植户所有租地方案.
考点:一元一次不等式组的应用;二元一次方程组的应用。
专题:应用题;图表型。
分析:(1)根据等量关系:甲种植户总收入为12500元,乙种植户总收入为16500元,列出方程组求解即可;
(2)根据总收入不低于63000元,种植A类蔬菜的面积多于种植B类蔬菜的面积列出不等式组求解即可.
解答:解:(1)设A、B两类蔬菜每亩平均收入分别是x元,y元.
由题意得: (3分)
(3分)
解得:
答:A、B两类蔬菜每亩平均收入分别是3000元,3500元.(5分)
(2)设用来种植A类蔬菜的面积a亩,则用来种植B类蔬菜的面积为(20﹣a)亩.由题意得:
 (7分)
(7分)
解得:10<a≤14.
∵a取整数为:11、12、13、14.(8分)
∴租地方案为:
|
类别 |
种植面积
单位:(亩) |
|||
|
A |
11 |
12 |
13 |
14 |
|
B |
9 |
8 |
7 |
6 |
(10分)
说明:依据此评分标准,其它方法写出租地方案均可得分.
点评:考查了二元一次方程组的应用和一元一次不等式组的应用,读懂统计表,能够从统计表中获得正确信息,及熟练解方程组和不等式组是解题的关键.
22、(2011•潼南县)端午节吃粽子是中华民族的传统习俗,一超市为了吸引消费者,增加销售量,特此设计了一个游戏,其规则是:分别转动如图所示的两个可以自由转动的转盘各一次,每次指针落在每一字母区域的机会均等(若指针恰好落在分界线上则重转),当两个转盘的指针所指字母都相同时,消费者就可以获得一次八折优惠价购买粽子的机会.

(1)用树状图或列表的方法(只选其中一种)表示出游戏可能出现的所有结果;
(2)若一名消费者只能参加一次游戏,则他能获得八折优惠价购买粽子的概率是多少?
考点:列表法与树状图法。
分析:(1)根据题意此题需要两步完成,所以采用树状图法或者采用列表法都比较简单;注意要做到不重不漏;
(2)依据表格或树状图分析所有等可能的出现结果,然后根据概率公式即可求出该事件的概率.
解答:解:(1)解法一:

解法二:
|
转盘2 转盘1 |
C |
D |
|
A |
(A,C) |
(A,D) |
|
B |
(B,C) |
(B,D) |
|
C |
(C,C) |
(C,D) |
(2)∵一共有6种等可能的结果,当两个转盘的指针所指字母都相同时的结果有一个,
∴P= .
.
点评:本题考查的是用列表法或画树状图法求概率.列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件.用到的知识点为:概率=所求情况数与总情况数之比.
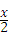 B、
B、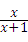
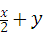 D、
D、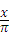

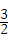 ,
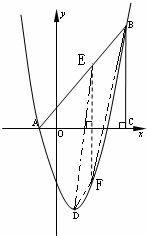
, ),点D的坐标为(1,﹣4)由S四边形EBFD=S△BEF+S△DEF即可求得;
),点D的坐标为(1,﹣4)由S四边形EBFD=S△BEF+S△DEF即可求得; ,即可求得点P的坐标,又由过点F作b⊥EF交抛物线于P3,设P3(n,n2﹣2n﹣3),可得n2﹣2n﹣2=﹣
,即可求得点P的坐标,又由过点F作b⊥EF交抛物线于P3,设P3(n,n2﹣2n﹣3),可得n2﹣2n﹣2=﹣ ,求得点P的坐标,则可得使△EFP是以EF为直角边的直角三角形的P的坐标.
,求得点P的坐标,则可得使△EFP是以EF为直角边的直角三角形的P的坐标. ,
,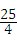 ,
, ×
×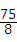 ;
;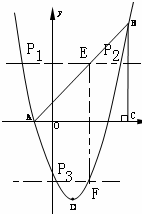 ②如图:
②如图: ,m2=
,m2=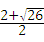 ,
,

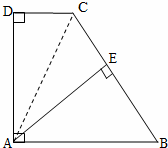
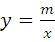 (m≠0)的图象相交于A、B两点.求:
(m≠0)的图象相交于A、B两点.求:
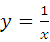 (4分)
(4分)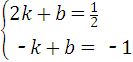
 (6分)
(6分)
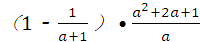 ,其中a=
,其中a=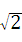 ﹣1.
﹣1. •
• ,(4分)
,(4分)
