|
标准方程 |
 ( ( ) ) |
  ( ( ) ) |
 (  ) ) |
 (  ) ) |
|
图形 |
 |
|
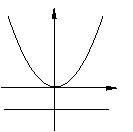 |
 |
|
范围 |
 ≥ ≥ , , |
 ≤ ≤ , , |
 ≥ ≥ , , |
 ≤ ≤ , , |
|
焦点 |
 |
 |
 |
 |
|
准线 |
 |
 |
 |
 |
|
焦半径 |
 |
 |
 |
 |
|
对称轴 |
 轴 轴 |
 轴 轴 |
||
|
顶点 |
 |
|||
|
离心率 |
 |
 (课本
(课本 )
) (
( )的几何意义是抛物线的焦准距(焦点到准线的距离).
)的几何意义是抛物线的焦准距(焦点到准线的距离).
 (课本
(课本 )抛物线的通径:通过焦点并且垂直于对称轴的直线与抛物线两交点之间的线段叫做抛物线的通径.通径的长为
)抛物线的通径:通过焦点并且垂直于对称轴的直线与抛物线两交点之间的线段叫做抛物线的通径.通径的长为 ,通径是过焦点最短的弦.
,通径是过焦点最短的弦.
|
定义 |
 到两个定点 到两个定点 与 与 的距离之差的绝对值等于定长( 的距离之差的绝对值等于定长( )的点的轨迹 )的点的轨迹 到定点 到定点 与到定直线 与到定直线 的距离之比等于常数 的距离之比等于常数 ( ( )的点的轨迹 )的点的轨迹 |
||
|
标准方程 |
 ( ( ) ) |
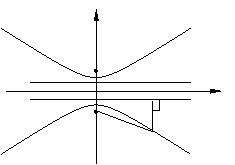  ( ( ) ) |
|
|
简图 |
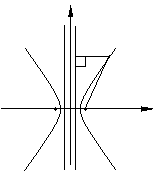 |
|
|
|
几何性质 |
焦点坐标 |
 , , |
 , , |
|
顶点 |
 , , |
 , , |
|
|
范围 |
 ≥ ≥ , , |
 ≥ ≥ , , |
|
|
准线 |
 |
 |
|
|
渐近线方程 |
 |
 |
|
焦半径 |
 , ,  在左支上用“ 在左支上用“ ”, ”, 在右支上用“ 在右支上用“ ” ” |
 , ,  在下支上用“ 在下支上用“ ”, ”, 在上支上用“ 在上支上用“ ” ” |
|
|
对称性 |
关于 轴均对称,关于原点中心对称; 轴均对称,关于原点中心对称; |
||
|
离心率 |
 |
||
 的关系 的关系 |
 |
||
焦点三角形 的面积: 的面积: ( ( , , 为虚半轴长) 为虚半轴长) |
 与
与 共渐近线的双曲线方程
共渐近线的双曲线方程 -
- (
( ).
).
 与
与 有相同焦点的双曲线方程
有相同焦点的双曲线方程 -
- (
( 且
且 )
)
 双曲线形状与
双曲线形状与 的关系:
的关系:
 ,
, 越大,即渐近线的斜率的绝对值就越大,这时双曲线的形状就从扁狭逐渐变得开阔,即双曲线的离心率越大,它的开口就越阔.
越大,即渐近线的斜率的绝对值就越大,这时双曲线的形状就从扁狭逐渐变得开阔,即双曲线的离心率越大,它的开口就越阔.
 过点
过点 ;
; 焦点在直线
焦点在直线 上;
上; 顶点在原点,对称轴为
顶点在原点,对称轴为 到焦点的距离等于
到焦点的距离等于 ;
; 所得弦长为
所得弦长为 .
. 上找一点
上找一点 ,使
,使 最小,其中
最小,其中 ,
, ,求
,求 ,抛物线上有一动点
,抛物线上有一动点 ,
, ,求
,求 的最小值及此时
的最小值及此时 全国Ⅱ)抛物线
全国Ⅱ)抛物线 上一点
上一点 的纵坐标为
的纵坐标为 ,则点
,则点
 海南)已知抛物线
海南)已知抛物线 的焦点为
的焦点为 ,点
,点 ,
, 在抛物线上,且
在抛物线上,且 , 则有
, 则有



 的端点
的端点 上移动,求线段
上移动,求线段 距离的最小值是
距离的最小值是

 和
和 相交于点
相交于点 ,点
,点 为锐角三角形,
为锐角三角形, ,
, ,且
,且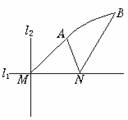
 ,
, 两点在抛物线
两点在抛物线 上,
上, 是
是 取何值时,直线
取何值时,直线 (
( 湖南)如果双曲线
湖南)如果双曲线 ,那么点
,那么点


 -
- (
( ,
, )的右焦点为
)的右焦点为 的面积为
的面积为
 陕西)已知双曲线
陕西)已知双曲线 )的两条渐近线的夹角为
)的两条渐近线的夹角为 ,则双曲线的离心率为
,则双曲线的离心率为 





 分别是双曲线
分别是双曲线 且
且

 (
( ,则双曲线的离心率为
,则双曲线的离心率为 

 :
: 的左顶点
的左顶点 的直线
的直线 , 且
, 且 , 则双曲线
, 则双曲线

 与曲线
与曲线
 的
的 的右焦点为圆心,且与其右准线相切的圆的方程是
的右焦点为圆心,且与其右准线相切的圆的方程是





 是该双曲线的两个焦点,
是该双曲线的两个焦点, ,则
,则
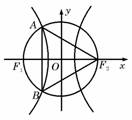
 和
和 分别是双曲线
分别是双曲线 的两个焦点,
的两个焦点, 为半径的圆与该双曲线左支的两个交点,且
为半径的圆与该双曲线左支的两个交点,且
 中,双曲线中心在原点,焦点在
中,双曲线中心在原点,焦点在 轴上,一条渐近线方程为
轴上,一条渐近线方程为 ,则它的离心率为
,则它的离心率为 两点,
两点, 的值为
的值为
 设动点
设动点 和
和 的距离分别为
的距离分别为 ,且存在常数
,且存在常数 ,使得
,使得 .
. 证明:动点
证明:动点 过点
过点 ,其中点
,其中点 (
( 的
的 .
. 的渐近线方程是
的渐近线方程是 ,且焦距为
,且焦距为

 ,则
,则


 表示焦点在
表示焦点在 的范围是
的范围是
 ,则
,则 及圆
及圆 作直线
作直线

 分别是双曲线
分别是双曲线 是双曲线左支上过点
是双曲线左支上过点 的弦,
的弦, ,则
,则 的周长是
的周长是
 ,
, 成等差数列,求
成等差数列,求 、
、 ,到
,到 ;
; ;
; 以椭圆
以椭圆 的长轴端点为焦点,且过点
的长轴端点为焦点,且过点 ;
; ,且一条渐近线方程为
,且一条渐近线方程为 ;
; ,且过点
,且过点 ,①求
,①求 的最小值;②求
的最小值;②求 的最小值.
的最小值.  问题3.已知双曲线方程为
问题3.已知双曲线方程为 ,
, 的平分线交
的平分线交 ,求双曲线方程.
,求双曲线方程. 为右焦点,
为右焦点, 与渐近线
与渐近线 的长是焦点
的长是焦点 ,且双曲线的离心率
,且双曲线的离心率 ,
, 交左准线于
交左准线于 的中点,
的中点, 与双曲线
与双曲线 与右支有两个交点
与右支有两个交点 (
( 新课程)椭圆
新课程)椭圆 的一个焦点是
的一个焦点是 ,那么
,那么
 上一点
上一点 到左准线的距离为
到左准线的距离为 ,
, 是该椭圆的左焦点,若点
是该椭圆的左焦点,若点 满足
满足 ,则
,则
 中,已知
中,已知 顶点
顶点 和
和 ,顶点
,顶点
 北京春)椭圆
北京春)椭圆 的离心率为
的离心率为 


 倍,则椭圆的离心率等于
倍,则椭圆的离心率等于
 分别是椭圆
分别是椭圆 (
( )的左、右焦点,
)的左、右焦点, (
( 为半焦距)的点,且
为半焦距)的点,且 ,则椭圆的离心率是
,则椭圆的离心率是
 的焦点为
的焦点为 轴的交点分别
轴的交点分别 ,若
,若 ≤
≤ ,则该椭圆离心率的取值范围是
,则该椭圆离心率的取值范围是



 (
( 是右焦点为
是右焦点为 成等差数列”是“
成等差数列”是“ ”的
”的 ,
, 为焦点的椭圆与直线
为焦点的椭圆与直线 有且仅有
有且仅有


 在椭圆
在椭圆 上,顶点
上,顶点


 ,右焦点为
,右焦点为 ,方程
,方程 的两个实根分别为
的两个实根分别为 和
和 ,则点
,则点 内
内 与椭圆
与椭圆 记
记 的面积为
的面积为 .
. 求在
求在 ,
, 的条件下,
的条件下, 当
当 ,
, 时,求直线
时,求直线 的方程.
的方程. 分别是椭圆
分别是椭圆 的最大值和最小值;
的最大值和最小值;  的直线
的直线 与椭圆交于不同的两点
与椭圆交于不同的两点 为锐角(其中
为锐角(其中 为作标原点),求直线
为作标原点),求直线 ,
, 的距离为
的距离为 .(Ⅰ)证明
.(Ⅰ)证明 ;
; 上任意点
上任意点 处的切线交
处的切线交 两点,则
两点,则 上任意一点,
上任意一点, 表示焦点在
表示焦点在 轴的椭圆,那么实数
轴的椭圆,那么实数 公里,远地点为约
公里,远地点为约 公里。设地球的半经为
公里。设地球的半经为 表示的曲线是
表示的曲线是  ,
, 满足:
满足: ,则
,则
 是椭圆
是椭圆 的两个焦点,
的两个焦点, ,
, 的面积最大,则有
的面积最大,则有



 的取值范围是
的取值范围是

 都与椭圆
都与椭圆 ,与椭圆
,与椭圆 ,且
,且 ,求椭圆方程.
,求椭圆方程. ,
, ;
; 和椭圆
和椭圆 和
和
 的左焦点,
的左焦点, 是一
是一 的最小值,并求点
的最小值,并求点 的最大值和最小值.
的最大值和最小值. 在椭圆
在椭圆 上,求
上,求 为钝角时,
为钝角时, .
. )
) (
( ,
, ,到相应准线的距离为
,到相应准线的距离为