网址:http://m.1010jiajiao.com/timu_id_4389672[举报]
(本小题满分12分)
如图所示茎叶图是青年歌手电视大奖赛中7位评委给参加最后决赛的两位选手甲、乙评定的成绩,程序框图用来编写程序统计每位选手的成绩(各评委所给有效分数的平均值),试根据下面条件回答下列问题:
1)根据茎叶图,乙选手的成绩中,中位数是 ,众数是 。
2)在程序框图中,用k表示评委人数,用a表示选手的最后成绩(各评委所给有效分数的平均值)那么图中①②处分别为 , 。“S1=S-max-min”的含义
” 。
3) 根据程序框图,甲的最后成绩是 ;乙的最后成绩是 。

查看习题详情和答案>>
 .如图所示的茎叶图是青年歌手电 甲 乙
.如图所示的茎叶图是青年歌手电 甲 乙
视大奖赛中7位评委给参加最后决赛的两位选手 8 5 7 9
甲、乙评定的成绩,程序框图用来编写程序统计 8 5 5 4 8 4 4 4 6 7
每位选手的成绩(各评委所给有效分数的平均值), 2 9 3
试根据下面条件回答下列问题:
1)根据茎叶图,乙选手的成绩中,中位数是 , 众数是 。
2)在程序框图中,用k表示评委人数,用a 表示选手的最后成绩(各评委所给有效分数的平均值)那么图中①②处分别应填 , 。
“S1=S-max-min”的含义 是 。
3) 根据程序框图,甲的最后成绩是 ;乙的最后成绩是 。

查看习题详情和答案>>
本题有3小题,第1小题5分,第2小题5分,第3小题9分.
已知定义在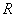 上的函数
上的函数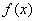 和数列
和数列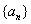 满足下列条件:
满足下列条件:
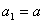 ,
,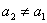 ,当
,当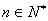 且
且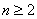 时,
时,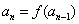 且
且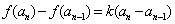 .
.
其中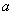 、
、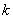 均为非零常数.
均为非零常数.
(1)若数列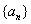 是等差数列,求
是等差数列,求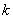 的值;
的值;
(2)令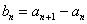
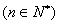 ,若
,若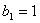 ,求数列
,求数列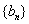 的通项公式;
的通项公式;
(3)试研究数列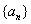 为等比数列的条件,并证明你的结论.
为等比数列的条件,并证明你的结论.
说明:对于第3小题,将根据写出的条件所体现的对问题探究的完整性,给予不同的评分。
查看习题详情和答案>>