 每个面都是有相同边数的正多边形,每个顶点为端点都有相同棱数的凸多面体,叫做正多面体.
每个面都是有相同边数的正多边形,每个顶点为端点都有相同棱数的凸多面体,叫做正多面体.
 正多面体有且只有
正多面体有且只有 种.分别是正四面体、正六面体、正八面体、正十二面体、正二十面体.
种.分别是正四面体、正六面体、正八面体、正十二面体、正二十面体.
 简单多面体:考虑一个多面体,例如正六面体,假定它的面是用橡胶薄膜做成的,如果充以气体,那么它就会连续(不破裂)变形,最后可变为一个球面.如图:象这样,表面经过连续变形可变为球面的多面体,叫做简单多面体.
简单多面体:考虑一个多面体,例如正六面体,假定它的面是用橡胶薄膜做成的,如果充以气体,那么它就会连续(不破裂)变形,最后可变为一个球面.如图:象这样,表面经过连续变形可变为球面的多面体,叫做简单多面体.
说明:棱柱、棱锥、正多面体等一切凸多面体都是简单多面体
 五种正多面体的顶点数、面数及棱数:
五种正多面体的顶点数、面数及棱数:
|
正多面体 |
顶点数 |
面数 |
棱数 |
|
正四面体 |
 |
 |
 |
|
正六面体 |
 |
 |
 |
|
正八面体 |
 |
 |
 |
|
正十二面体 |
 |
 |
 |
|
正二十面体 |
 |
 |
 |
 欧拉定理(欧拉公式):简单多面体的顶点数
欧拉定理(欧拉公式):简单多面体的顶点数 、面数
、面数 及棱数
及棱数 有关系式:
有关系式:
 计算棱数
计算棱数 常见方法:
常见方法:
 ;
;
 各面多边形边数和的一半;
各面多边形边数和的一半;
 顶点数与共顶点棱数积的一半.
顶点数与共顶点棱数积的一半.
 球的概念: 与定点距离等于或小于定长的点的集合,叫做球体,简称球
球的概念: 与定点距离等于或小于定长的点的集合,叫做球体,简称球 定点叫球心,定长叫球的半径
定点叫球心,定长叫球的半径 与定点距离等于定长的点的集合叫做球面.一个球或球面用表示它的球心的字母表示,例如球
与定点距离等于定长的点的集合叫做球面.一个球或球面用表示它的球心的字母表示,例如球
 球的截面:用一平面
球的截面:用一平面 去截一个球
去截一个球 ,设
,设 是平面
是平面 的垂线段,
的垂线段, 为垂足,且
为垂足,且 ,所得的截面是以球心在截面内的射影为圆心,以
,所得的截面是以球心在截面内的射影为圆心,以 为半径的一个圆,截面是一个圆面.
为半径的一个圆,截面是一个圆面.
球面被经过球心的平面截得的圆叫做大圆,被不经过球心的平面截得的圆叫做小圆
 两点的球面距离:球面上两点之间的最短距离,就是经过两点的大圆在这两点间的一段劣弧的长度,我们把这个弧长叫做两点的球面距离.
两点的球面距离:球面上两点之间的最短距离,就是经过两点的大圆在这两点间的一段劣弧的长度,我们把这个弧长叫做两点的球面距离. (
( 为球心角的弧度数).
为球心角的弧度数).
 球的表面积和体积公式:
球的表面积和体积公式: ,
, .
.
 (
( 湖南)棱长为
湖南)棱长为 的正方体
的正方体 的
的 个顶点都在球
个顶点都在球 分别是棱
分别是棱 ,
, 的中点,则直线
的中点,则直线 被球
被球




 .(
.( 沿对角线
沿对角线 折成直二面角,折成直二面角后,在
折成直二面角,折成直二面角后,在 四点所在的球面上,
四点所在的球面上, 与
与 两点之间的球面距离为
两点之间的球面距离为



 的棱长为
的棱长为 的垂线,垂足为点
的垂线,垂足为点 ,则以下命题中,错误的命题是
,则以下命题中,错误的命题是 的垂心
的垂心 垂直平面
垂直平面



 中,
中, ,
, ,
, ,
, 与底面
与底面 所成的二面角为
所成的二面角为 ,
, 分别是棱
分别是棱 、
、 求
求 证明:
证明: ;
; 求经过
求经过 四点的球的体积.
四点的球的体积. 将正方形折成正四棱柱的侧面,正方形的对角线
将正方形折成正四棱柱的侧面,正方形的对角线 ,则
,则
 ,
, ,
, ,
,

 的正三棱锥
的正三棱锥 的外接球
的外接球 ,则其外接球
,则其外接球 及数字作答,不能含
及数字作答,不能含 ;类比到平面的情形:若
;类比到平面的情形:若 内一点,有
内一点,有 ;类比到空间的情形:若
;类比到空间的情形:若 条棱中,其中
条棱中,其中 ,则第
,则第


 (
( 所在的平面
所在的平面 和
和 垂直,且
垂直,且 ,
, ,
, ,则点
,则点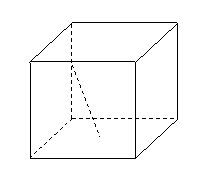 (
( 的
的 在棱
在棱

 ,则函数
,则函数


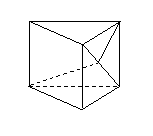 问题1. (
问题1. ( ,
, ,
, 的最小值
的最小值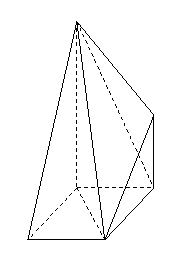 问题2.将如图
问题2.将如图 (图中所示数字为对应线段长度)沿直线
(图中所示数字为对应线段长度)沿直线 的大小;
的大小; 这五个点在同一球面上,求该球的表面积.
这五个点在同一球面上,求该球的表面积.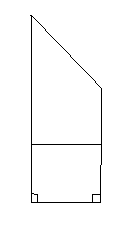
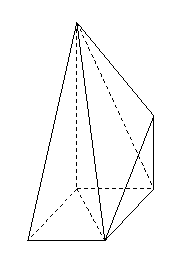
 为底面)被一平面所截得到的
为底面)被一平面所截得到的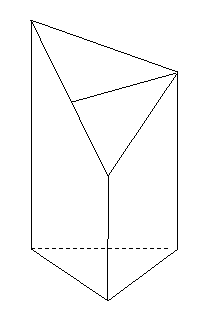 几何体,截面为
几何体,截面为 ,
, ,
, 的大小;
的大小;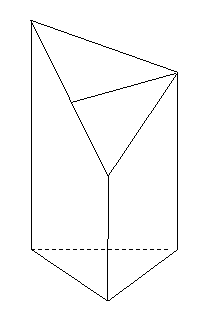
 问题4. (
问题4. ( ;点
;点 分别在
分别在 ,四棱锥
,四棱锥 与
与 ,求二面角
,求二面角 的平面角的正切值.
的平面角的正切值.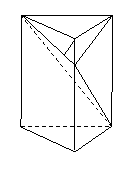
 的球面上,其中底面的三个顶点在该球的一个大圆上,则该正三棱锥的体积是
的球面上,其中底面的三个顶点在该球的一个大圆上,则该正三棱锥的体积是 


 ,棱长为
,棱长为 的正六棱柱的所有顶点都在一个平面上,则此球的体积为
的正六棱柱的所有顶点都在一个平面上,则此球的体积为
 (
( 的球面上。如果正四棱柱的底面边长为
的球面上。如果正四棱柱的底面边长为 ,那么该棱柱的表面积为
,那么该棱柱的表面积为

 的椭圆,则制作这个广告气球至少需要的面料是
的椭圆,则制作这个广告气球至少需要的面料是  、
、 两两互相垂直,且
两两互相垂直,且 ,那么这个球面的面积是
,那么这个球面的面积是 









 的正方体,连结相邻面的中心,以这些线段为棱的
的正方体,连结相邻面的中心,以这些线段为棱的
 的底面边长和各侧棱长都为
的底面边长和各侧棱长都为 ,点
,点
 的外接球球心在
的外接球球心在 ,
, ,
,

 的球,且相邻的球都相切(球心的连线构成正方形).在这
的球,且相邻的球都相切(球心的连线构成正方形).在这 问题3. (
问题3. ( ,且二面角
,且二面角 的大小为
的大小为

 的两条棱
的两条棱 ,其余各棱长均为
,其余各棱长均为 (
( 安徽)在正方体上任意选择
安徽)在正方体上任意选择 个顶点,它们可能是如下各种几何形体的
个顶点,它们可能是如下各种几何形体的 ,
, ,
,

 ,底面
,底面 ).用它们
).用它们 的取值范围是
的取值范围是
 ,则其体积为
,则其体积为
 高为
高为 ,则点
,则点 到侧面
到侧面 一个正三棱锥与一个正四棱锥,它们的棱长都相等,把这个正三棱锥的一个侧面重合在正四棱锥的一个侧面上,这个组合体可能是
一个正三棱锥与一个正四棱锥,它们的棱长都相等,把这个正三棱锥的一个侧面重合在正四棱锥的一个侧面上,这个组合体可能是 如果三棱锥
如果三棱锥 的底面是不等边三角形,侧面与底面所成的二面角相等,且
的底面是不等边三角形,侧面与底面所成的二面角相等,且 内,那么
内,那么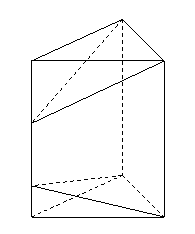
 中,
中, ,
, ,
, 为侧棱
为侧棱 上的两点,且
上的两点,且 ,
, 的体积等于
的体积等于
 ,则侧棱
,则侧棱 所成的角的大小是
所成的角的大小是
 ,和这条棱相对的棱长是
,和这条棱相对的棱长是 ,求棱锥的体积.
,求棱锥的体积.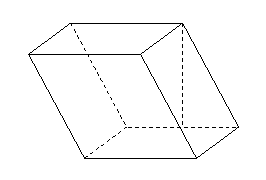
 的底面是矩形,
的底面是矩形, 在底面
在底面 上的射影
上的射影 是
是 与底面
与底面 为
为 作一平面与底面成
作一平面与底面成 所截得的线段长等于
所截得的线段长等于
 ,
,  ,
, ,
, ,
, 垂足为
垂足为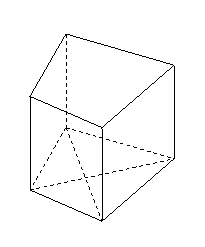
 求证:
求证: ;
; 求异面直线
求异面直线 与
与 所成的角.
所成的角.