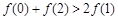摘要:定义 到两个定点与的距离之差的绝对值等于定长()的点的轨迹 到定点与到定直线的距离之比等于常数()的点的轨迹 标准方程 () () 简图 几何性质 焦点坐标 . . 顶点 . . 范围 ≥. ≥. 准线 渐近线方程 焦半径 . 在左支上用“ . 在右支上用“ . 在下支上用“ . 在上支上用“ 对称性 关于轴均对称.关于原点中心对称, 离心率 的关系 焦点三角形的面积:(.为虚半轴长) 与共渐近线的双曲线方程-(). 与有相同焦点的双曲线方程-(且) 双曲线形状与的关系:,越大.即渐近线的斜率的绝对值就越大.这时双曲线的形状就从扁狭逐渐变得开阔.即双曲线的离心率越大.它的开口就越阔.
网址:http://m.1010jiajiao.com/timu_id_4389675[举报]
有人说椭圆与双曲线是对偶曲线,如它们的定义中:“到两个定点的和为常数”、“到两个定点的差的绝对值为常数”;“常数大于|F1F2|”、“常数小于|F1F2|”具有对偶性.再列举出两条类似对偶性质: .
查看习题详情和答案>>
有人说椭圆与双曲线是对偶曲线,如它们的定义中:“到两个定点的和为常数”、“到两个定点的差的绝对值为常数”;“常数大于|F1F2|”、“常数小于|F1F2|”具有对偶性.再列举出两条类似对偶性质: .
查看习题详情和答案>>
椭圆的定义:平面内到两个定点F1、F2的距离之和等于常数(________|F1F2|)的点的集合叫作椭圆,这两个定点F1、F2叫作椭圆的________,两焦点间的距离叫作椭圆的________.
 到两定点
到两定点 的距离之和为4,则点
的距离之和为4,则点 上一点,
上一点, 为焦点,定点
为焦点,定点 ,则
,则 的最小值3;
的最小值3; 在
在 上单调递增;
上单调递增;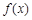 满足
满足 ,
, ,则
,则