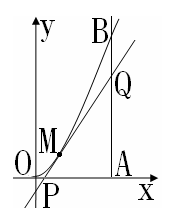
10.如图,曲线段OMB是函数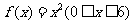 的图象,
的图象,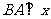 轴于点A,曲线段OMB上一点M
轴于点A,曲线段OMB上一点M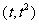 处的切线PQ交x轴于点P,交线段AB于点Q
处的切线PQ交x轴于点P,交线段AB于点Q
(1)若t已知,求切线PQ的方程 (2)求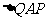 的面积的最大值
的面积的最大值
 解:(1)
解:(1)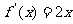 ,所以过点M的切线的斜率为
,所以过点M的切线的斜率为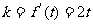
由点斜式得切线PQ方程为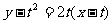 ,
,
即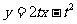 ……①
……①
(2)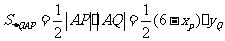 …………②
…………②
对①令x=6得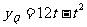 …………③
…………③
令y=0得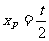 …………④
…………④
③④代入②得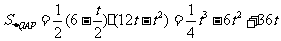
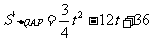 ,令
,令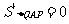 解得
解得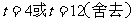
|
T |
(0,4) |
4 |
(4,6) |
|
S’ |
+ |
0 |
- |
|
S |
增 |
极大值64 |
减 |
所以当t=4时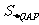 有极大值64,
有极大值64,
所以当t=4时,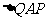 的面积的最大值为64.
的面积的最大值为64.
8.人教版选修1-1第108页B 组习题,选修2-2第34页B组习题
利用函数的单调性,证明: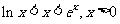
变式1:证明: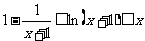 ,
,
证明:(1)构造函数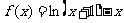 ,
,
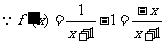
 ,当
,当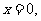
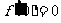 ,得下表
,得下表
|
|
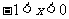 |
 |
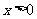 |
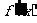 |
+ |
0 |
- |
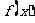 |
单调递增 |
极大值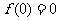 |
单调递减 |
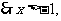 总有
总有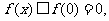
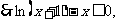
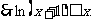
另解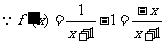
 ,当
,当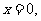
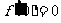 ,
,
当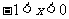 ,
,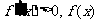 单调递增,
单调递增,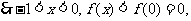 ……①
……①
当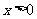 ,
,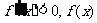 单调递减,
单调递减,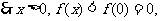 ………………②
………………②
当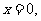
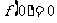 …………………………………………………………③
…………………………………………………………③
综合①②③得:当 时,
时,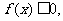
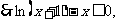
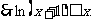
(2)构造函数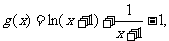
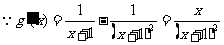 ,
,
当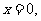
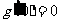 ,当
,当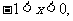
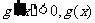 单调递减;
单调递减;
当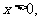
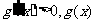 单调递增;
单调递增;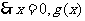 极小值=
极小值=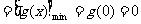 ,
,
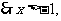 总有
总有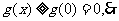
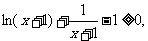 即:
即: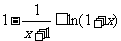 .
.
综上(1)(2)不等式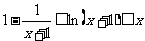 成立.
成立.
变式:(理科)设函数f(x)=(1+x)2-ln(1+x)2.若关于x的方程f(x)=x2+x+a在[0,2]上恰好有两个相异的实根,求实数a的取值范围.
解:
方程f(x)=x2+x+a, 即x-a+1-ln(1+x)2=0,记g(x)=x-a+1-ln(1+x)2.
所以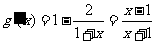 .由
.由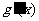 >0,得x<-1或x>1,由
>0,得x<-1或x>1,由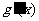 <0
<0
得-1<x<1.
所以g(x)在[0,1]上递减,在[1,2]上递增,为使f(x)=x2+x+a在[0,2]上恰好有两个相异的实根,只须g(x)=0在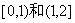 上各有一个实根,于是有
上各有一个实根,于是有

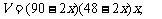 (0 < x < 24)
(0 < x < 24)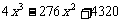 x
x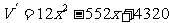 x
x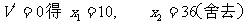
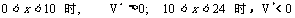
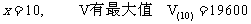
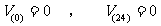
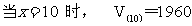 0
0
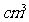
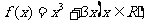 若
若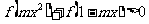 恒成立,求实数
恒成立,求实数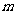 的取值范围
的取值范围
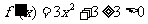 ,得
,得
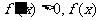 单调递增;
单调递增;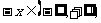
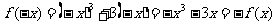 ,
,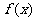 是奇函数.
是奇函数.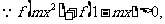
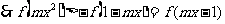 ,
,
 上单调递增,
上单调递增,  恒成立,即:
恒成立,即: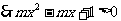 恒成立,分类:①当
恒成立,分类:①当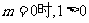 恒成立,
恒成立,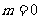 适合;
适合;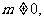
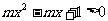 恒成立
恒成立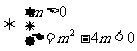 解得:
解得: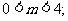
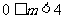
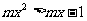 恒成立的条件实际上依然用的是函数图像(数形结合)的函数思想.
恒成立的条件实际上依然用的是函数图像(数形结合)的函数思想.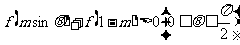 恒成立,求实数
恒成立,求实数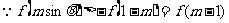 ,
,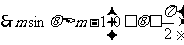 恒成立,即
恒成立,即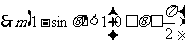 恒成立.
恒成立.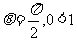 成立;
成立;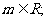 ②当
②当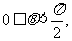
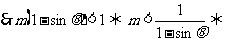
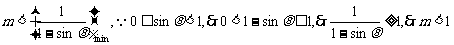
 (x)=0,此时函数在这点有极大(小)值,那么不与端点比较,也可以知道这就是最大(小)值.
(x)=0,此时函数在这点有极大(小)值,那么不与端点比较,也可以知道这就是最大(小)值.