摘要： 函数若恒成立,求实数的取值范围 解:由.得单调递增, 又. 所以是奇函数.. 在上单调递增. 恒成立.即:恒成立.分类:①当恒成立.适合, ②当恒成立解得: 综上. 说明:(1)通过研究函数的性质.利用函数的性质解决不等式问题.是函数思想的重要应用.(2)找寻使恒成立的条件实际上依然用的是函数图像的函数思想. 变式:设函数若恒成立.求实数的取值范围. 解:由.得单调递增, 又. 所以是奇函数.. 恒成立.即恒成立. ①当成立,②当
网址：http://m.1010jiajiao.com/timu3_id_516188[举报]
函数f（x）=aex，g（x）=lnx-lna，其中a为常数，且函数y=f（x）和y=g（x）的图象在其与坐标轴的交点处的切线互相平行
（1）求函数y=g（x）的解析式；
（2）若关于x的不等式
＞
恒成立，求实数m的取值范围．
查看习题详情和答案>>
（1）求函数y=g（x）的解析式；
（2）若关于x的不等式
| x-m |
| g(x) |
| x |
函数y=f（x）的定义域D={x|x∈R，且x≠0}，对定义域D内任意两个实数x1，x2，都有f（x1）+f（x2）=f（x1x2）成立．
（1）求f（-1）的值并证明y=f（x）为偶函数；
（2）若f（-4）=4，记 an=(-1)n•f(2n)
，求数列{an}的前2009项的和S2009；
（3）（理） 若x＞1时，f（x）＜0，且不等式f(
)≤f(
)+f(a)对任意正实数x，y恒成立，求非零实数a的取值范围．
（4）（文） 若x＞1时，f（x）＜0，解关于x的不等式 f（x-3）≥0．
查看习题详情和答案>>
（1）求f（-1）的值并证明y=f（x）为偶函数；
（2）若f（-4）=4，记 an=(-1)n•f(2n)
|
（3）（理） 若x＞1时，f（x）＜0，且不等式f(
| x2+y2 |
| xy |
（4）（文） 若x＞1时，f（x）＜0，解关于x的不等式 f（x-3）≥0．
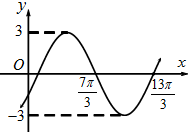函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，
，若点
在函数
的图象上，则点
在函数
的图象上. w.w.w.k.s.5.u.c.o.m 
的解析式；
恒有
成立，求实数
的取值范围.
.
，求
的解析式；
在
上恒成立，求实数
的取值范围.