0 51550 51558 51564 51568 51574 51576 51580 51586 51588 51594 51600 51604 51606 51610 51616 51618 51624 51628 51630 51634 51636 51640 51642 51644 51645 51646 51648 51649 51650 51652 51654 51658 51660 51664 51666 51670 51676 51678 51684 51688 51690 51694 51700 51706 51708 51714 51718 51720 51726 51730 51736 51744 447348
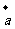 =(h,k)(其中h>0,k>0)平移,就是将图形F( )
=(h,k)(其中h>0,k>0)平移,就是将图形F( )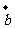 为不共线向量,
为不共线向量,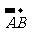 =
=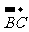 =-4
=-4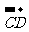 =
=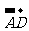 =
=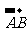 =
=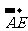 =
=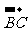 =( )
=( )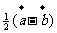 (B)
(B) 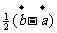 (C)
(C) 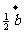 (D)
(D) 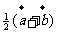
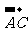 =
=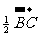 (C)
(C) 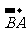 =
=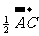
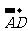 =
=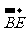 =( )
=( )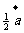 (B)
(B)
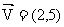 ,当t=0时,P在(-6,-2)处,则t=5时,点P的坐标为________
,当t=0时,P在(-6,-2)处,则t=5时,点P的坐标为________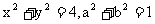 ,试求
,试求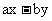 的取值范围。
的取值范围。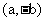 , q
, q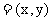 , p与q的交角为θ
, p与q的交角为θ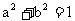 矛盾。同理q≠0)
矛盾。同理q≠0)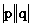 cosθ=
cosθ=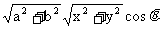 =2 cosθ
=2 cosθ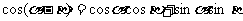
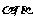
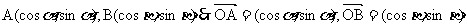
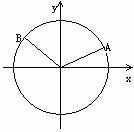 ∴
∴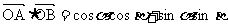
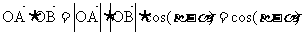
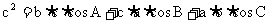
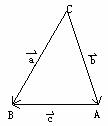 试判断此三角形的形状。
试判断此三角形的形状。
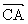 =b ,
=b ,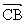 =a ,
=a ,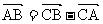 =a-b=c
=a-b=c ,
,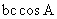 =-
=-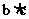 ,
, 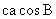 =
=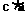 ,
, 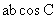 =
=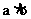
 从而
从而
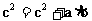 ∴
∴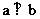
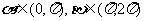 ,向量a=
,向量a=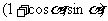 ,b=
,b=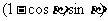
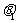 ,b与c的夹角为
,b与c的夹角为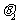 ,且
,且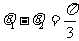 ,
,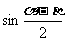 的值
的值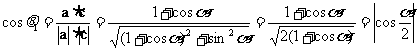
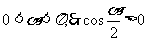 ∴
∴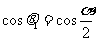
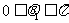 于是
于是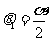
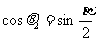 , 因而
, 因而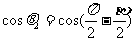
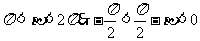 ,而
,而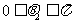 于是
于是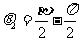
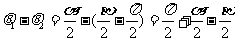
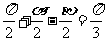 ∴
∴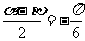 ∴
∴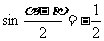
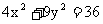 的焦点为
的焦点为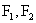 ,点P为其上的动点,当
,点P为其上的动点,当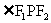 为钝角时,点P横坐标的取值范围是
为钝角时,点P横坐标的取值范围是
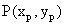 ,则
,则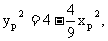
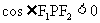 从而
从而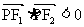
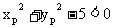 即
即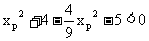
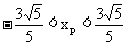
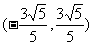
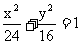 ,直线L:
,直线L: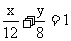 ,P是L上的点,射线OP交C于点
,P是L上的点,射线OP交C于点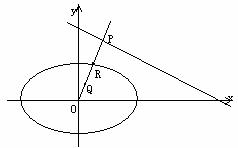 R,又点Q在OP上,且满足
R,又点Q在OP上,且满足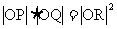 ,当点P在L上移动时,求点Q的方程。(95年全国高考题)
,当点P在L上移动时,求点Q的方程。(95年全国高考题)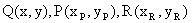
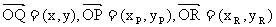
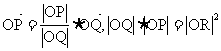
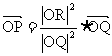
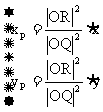 代入L方程得
代入L方程得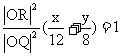
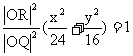 ∴
∴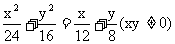
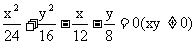
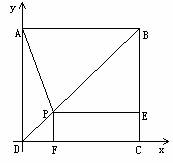 分析:如果用平面几何的常规证法来处理这两个结论,
分析:如果用平面几何的常规证法来处理这两个结论,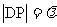 ,
,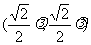 ,E
,E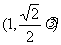 ,F
,F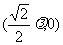
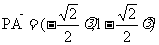
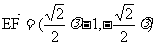
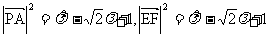 ∴
∴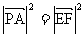 ∴PA=EF
∴PA=EF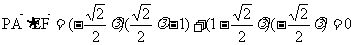
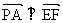 ∴PA⊥EF
∴PA⊥EF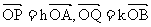 ,△OAB和△OPQ的面积分别为S和T。
,△OAB和△OPQ的面积分别为S和T。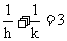 (2)
(2)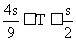
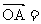 a,
a,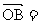 b
b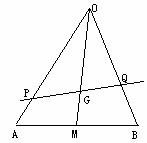 ∴
∴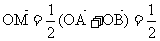 (a+ b)
(a+ b)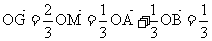 (a+ b)
(a+ b)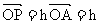 a ,
a ,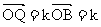 b
b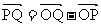 =kb-h a
=kb-h a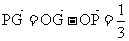 (a+ b)―h a=
(a+ b)―h a=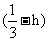 a+
a+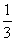 b
b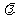 使得
使得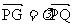
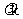 b-
b-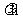 a
a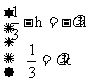 消去
消去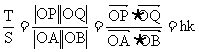
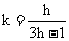 由于
由于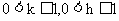
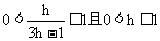 ∴
∴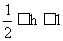
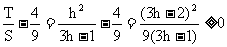 ∴
∴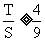
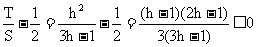 ∴
∴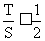
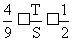 即
即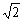 ,0)为圆心,1为半径的圆相切,双曲线的一个顶点A1与A点关于直线y=x对称. (1)求双曲线C的方程.
,0)为圆心,1为半径的圆相切,双曲线的一个顶点A1与A点关于直线y=x对称. (1)求双曲线C的方程. =1,解得k=±1.
=1,解得k=±1. ,依题意B点在平行的直线l′上,
,依题意B点在平行的直线l′上,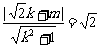 ,化简得m2+2
,化简得m2+2 ,解设m=
,解设m= ,k=
,k=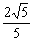 ,此时x=
,此时x= ,y=
,y=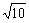 .故B(2
.故B(2