0 51519 51527 51533 51537 51543 51545 51549 51555 51557 51563 51569 51573 51575 51579 51585 51587 51593 51597 51599 51603 51605 51609 51611 51613 51614 51615 51617 51618 51619 51621 51623 51627 51629 51633 51635 51639 51645 51647 51653 51657 51659 51663 51669 51675 51677 51683 51687 51689 51695 51699 51705 51713 447348
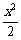 -2x+5.若对任意x∈[-1,2],都有f(x)>m,则实数m的取值范围是________.
-2x+5.若对任意x∈[-1,2],都有f(x)>m,则实数m的取值范围是________. (x)=3x2-x-2=0,x=1,-
(x)=3x2-x-2=0,x=1,-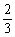 ,
,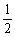 ,f(-
,f(-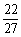 ,f(1)=3
,f(1)=3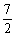 )
)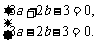
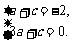
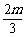 ,
,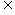 D,使f(x)在[a,b]上的值域也是[a,b].
D,使f(x)在[a,b]上的值域也是[a,b].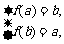 即
即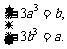
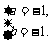 所求闭区间为[-1,1].
所求闭区间为[-1,1].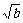 <1时,适合题意.
<1时,适合题意.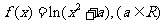
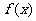 图象上点A
图象上点A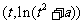 处的切线
处的切线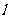 的方程;
的方程;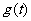 ,讨论
,讨论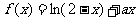 在
在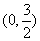 上是增函数,
上是增函数,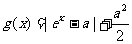 。当
。当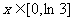 时,函数
时,函数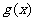 的最大值
的最大值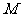 与
与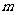 最小值的差为
最小值的差为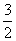 ,试求
,试求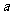 的值。
的值。