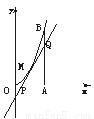
摘要：如图,曲线段OMB是函数的图象,轴于点A,曲线段OMB上一点M处的切线PQ交x轴于点P,交线段AB于点Q (1)若t已知,求切线PQ的方程 (2)求的面积的最大值 解:(1).所以过点M的切线的斜率为 由点斜式得切线PQ方程为. 即--① (2)----② 对①令x=6得----③ 令y=0得----④ ③④代入②得 .令 解得 T (0,4) 4 (4,6) S’ + 0 - S 增 极大值64 减 所以当t=4时有极大值64, 所以当t=4时,的面积的最大值为64.
网址：http://m.1010jiajiao.com/timu3_id_516189[举报]
如图所示,曲线段OMB是函数f(x)=x2(0＜x＜6)的图象,BA⊥x轴于点A,曲线段OMB上一点M(t,f(t))处的切线PQ交x轴于点P,交线段AB于点Q.
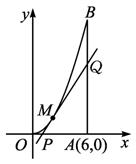
(1)试用t表示切线PQ的方程;
(2)设△QAP的面积为g(t);若函数g(t)在(m,n)上单调递减,试求出m的最小值;
(3)试求g(t)的取值范围.
查看习题详情和答案>>如图，曲线段OMB是函数f(x)＝x2(0≤x≤6)的图象，BA⊥x轴于点A，曲线段OMB上一点M(t，t2)处的切线PQ交x轴于点P，交线段AB于点Q
(1)若t已知，求切线PQ的方程
(2)求△QAP的面积的最大值
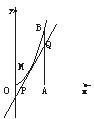如图所示，曲线段OMB是函数f（x）=x2（0＜x＜6）的图象，BA⊥x轴于A，曲线段OMB上一点M（t，f（t））处的切线PQ交x轴于P，交线段AB于Q，（1）试用t表示切线PQ的方程；
（2）试用t表示△QAP的面积g（t），若函数g（t）在[m，n]上单调递减，试求出m的最小值． 查看习题详情和答案>>
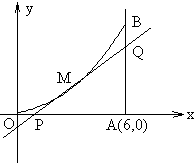如图所示，曲线段OMB是函数f（x）=x2（0＜x＜6）的图象，BA⊥x轴于A，曲线段OMB上一点M（t，f（t））处的切线PQ交x轴于P，交线段AB于Q，