0 51468 51476 51482 51486 51492 51494 51498 51504 51506 51512 51518 51522 51524 51528 51534 51536 51542 51546 51548 51552 51554 51558 51560 51562 51563 51564 51566 51567 51568 51570 51572 51576 51578 51582 51584 51588 51594 51596 51602 51606 51608 51612 51618 51624 51626 51632 51636 51638 51644 51648 51654 51662 447348
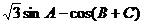 的值为:
的值为: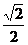 B.
B.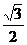 C.
C.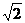 D.2
D.2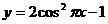 B.
B.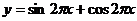
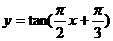 D.
D.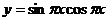
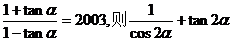 =
.
=
.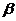 都是第二象限角,且
都是第二象限角,且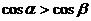 ,则:
,则: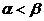 B.
B.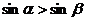 C.
C.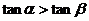 D.
D.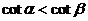
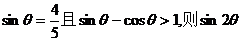 等于:
等于: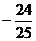 B.
B.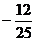 C.
C.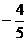 D.
D.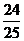
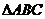 中,
中,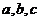 分别是角
分别是角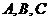 的对边,且
的对边,且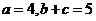 ,
,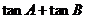 =
= ,求角A.
,求角A.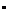 ,相距10海里C处的乙船,试问乙船应朝北偏东多少度的方向沿直线前往B处救援(角度精确到1
,相距10海里C处的乙船,试问乙船应朝北偏东多少度的方向沿直线前往B处救援(角度精确到1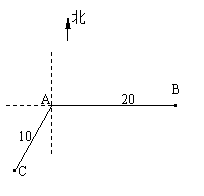 [解]
[解]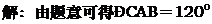
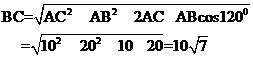 ………….5分
………….5分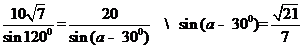 …8分
…8分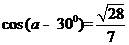 ……………………………………………………………………11分
……………………………………………………………………11分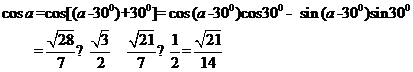 ………………14分
………………14分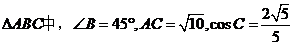 ,求(1)
,求(1)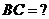
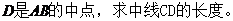

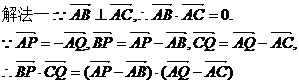
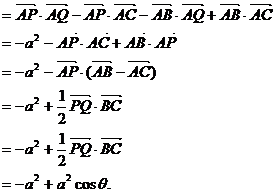
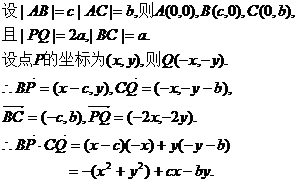
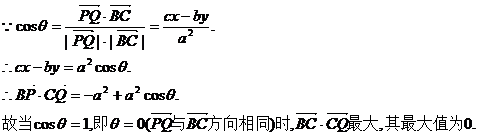
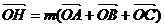 ,则实数m = 1
,则实数m = 1 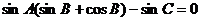
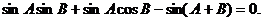
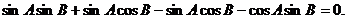
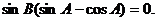
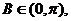 所以
所以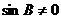 ,从而
,从而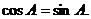
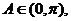 知
知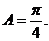 从而
从而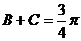 .
.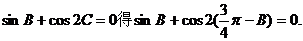
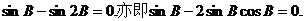
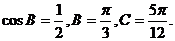 所以
所以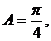
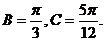
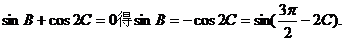
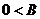 、
、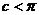 ,所以
,所以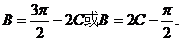 即
即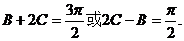
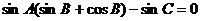 得
得 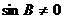 ,所以
,所以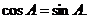
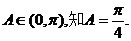 从而
从而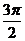 不合要求.
不合要求.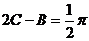 ,得
,得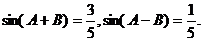
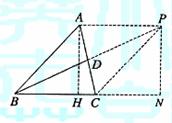
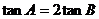 ; (Ⅱ)设AB=3,求AB边上的高.
; (Ⅱ)设AB=3,求AB边上的高.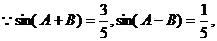
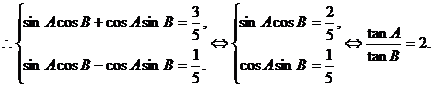
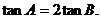
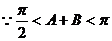 ,
,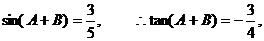
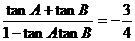 ,将
,将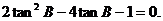
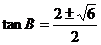 ,舍去负值得
,舍去负值得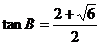 ,
, 设AB边上的高为CD.则AB=AD+DB=
设AB边上的高为CD.则AB=AD+DB=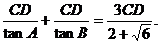
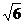 . 所以AB边上的高等于2+
. 所以AB边上的高等于2+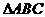 中,
中, ,
,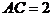 ,
,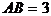 ,求
,求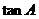 的值和
的值和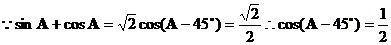 ,又
,又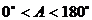
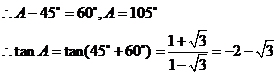
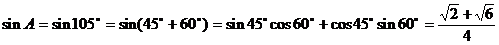
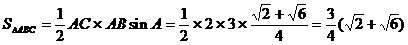
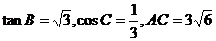 ,求△ABC的面积.
,求△ABC的面积.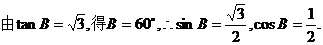
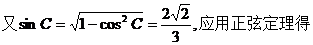
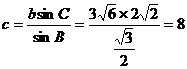 .
.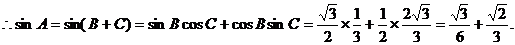
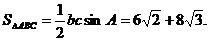
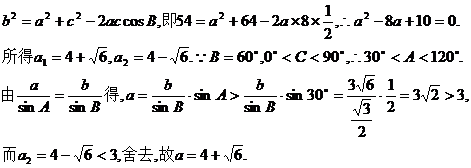
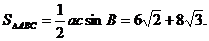
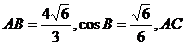 边上的中线BD=
边上的中线BD=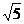 ,求sinA的值.
,求sinA的值.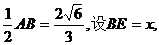
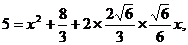
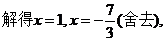
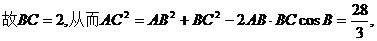
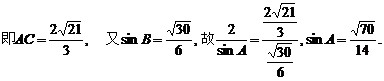
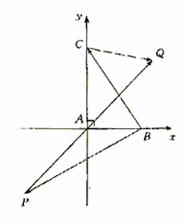
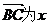 轴正向建立直角坐标系,且不妨设点A位于第一象限.
轴正向建立直角坐标系,且不妨设点A位于第一象限.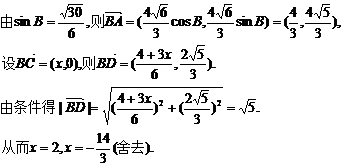
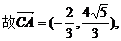
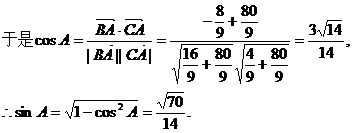
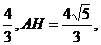

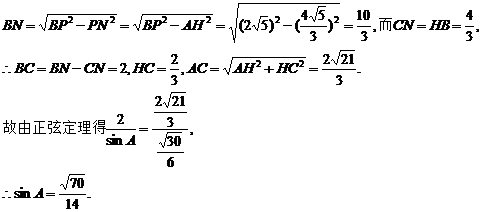
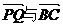
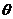 取何值时
取何值时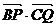 的值最大?并求出这个最大值.
的值最大?并求出这个最大值.