1.选择题(每小题5分,共50分)
(1)(07广东)已知集合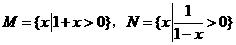 ,则
,则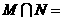 ( )
( )
A.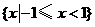 B.
B.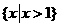 C.
C.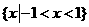 D.
D.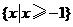
(2)(07广东)若函数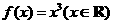 ,则函数
,则函数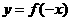 在其定义域上是( )
在其定义域上是( )
A.单调递减的偶函数 B.单调递减的奇函数
C.单调递增的偶函数 D.单调递增的奇函数
(3)(07山东)给出下列三个等式: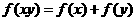 ,
,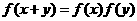 ,
, 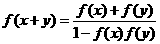 ,下列函数中不满足其中任何一个等式的是( )
,下列函数中不满足其中任何一个等式的是( )
A.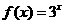 B.
B.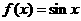 C.
C.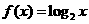 D.
D.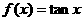
(4)已知函数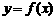 (
( )满足
)满足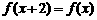 ,且当
,且当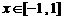 时,
时,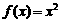 ,则
,则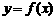 与
与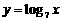 的图像的交点的个数为( )
的图像的交点的个数为( )
A.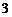 B.
B.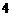 C.
C.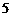 D.
D.
(5)设函数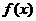 是定义在
是定义在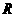 上的以3为周期的奇函数,若
上的以3为周期的奇函数,若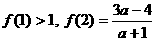 ,则a 的取值范围是
( )
,则a 的取值范围是
( )
A.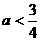 B.
B.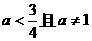 C.
C.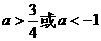 D.
D.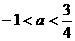
(6)设y=f (x)是定义在R上的奇函数, 当x≥0时, f (x)=x 2-2 x, 则在R上f (x)的表达式为 ( )
A. 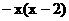 B.
B. 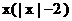 C.
C. 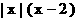 D.
D. 
(7) 二次函数f (x )满足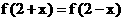 , 又f (x)在
, 又f (x)在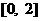 上是增函数, 且f(a)≥f(0), 那么实数a的取值范围是
( )
上是增函数, 且f(a)≥f(0), 那么实数a的取值范围是
( )
A. a≥0 B. a≤0 C. 0≤a≤4 D. a≤0或a≥4
(8) 函数y=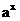 在
在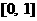 上的最大与最小值的和为3, 则a等于 ( )
上的最大与最小值的和为3, 则a等于 ( )
A. 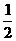 B.
2
C. 4 D.
B.
2
C. 4 D.
(9)若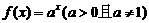 的反函数
的反函数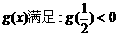 ,则函数
,则函数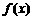 的图像向左平移一个单位后的图像大致是下图中的 ( )
的图像向左平移一个单位后的图像大致是下图中的 ( )
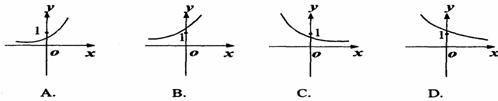
(10)若函数f(x)=x3+x2-2x-2的一个正数零点附近的函数值用二分法计算,其参考数据如下
|
f(1)=-2 |
f(1.5)=0.625 |
f(1.25)= -0.984 |
|
f(1.375)= -0.260 |
f(1.4375)=0.162 |
f(1.40625)= -0.054 |
那么方程x3+x2-2x-2=0的一个近似根(精确到0.1)为
A.1.2 B.1.3 C.1.4 D.1.5
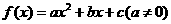 在闭区间
在闭区间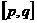 上的最值只能在
上的最值只能在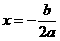 处及区间的两端点处取得,具体如下:
处及区间的两端点处取得,具体如下: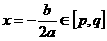 ,则
,则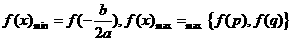 ;
;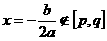 ,
,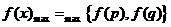 ,
,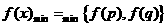 .
.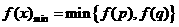 ,若
,若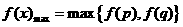 ,
,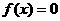 在
在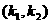 上有且只有一个实根,与
上有且只有一个实根,与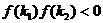 不等价,前者是后者的一个必要而不是充分条件.特别地,
方程
不等价,前者是后者的一个必要而不是充分条件.特别地,
方程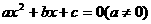 有且只有一个实根在
有且只有一个实根在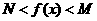
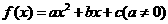 ;
;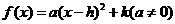 ;
;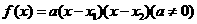 .
.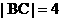 , BC的中点为M , 点A与B、C两点的距离之和为6, 设
, BC的中点为M , 点A与B、C两点的距离之和为6, 设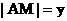 ,
, 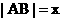 , 求
, 求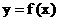 的函数表达式及其定义域.
的函数表达式及其定义域.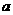 ,且不等式
,且不等式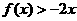 的解集为
的解集为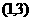 .(1)若方程
.(1)若方程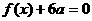 有两个相等的实根,求f
(x )的解析式;(2)若f (x )的最大值为正数,求
有两个相等的实根,求f
(x )的解析式;(2)若f (x )的最大值为正数,求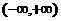 上的奇函数,对任意实数x,都有
上的奇函数,对任意实数x,都有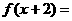
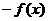 ,当
,当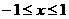 时,
时,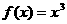 。(1)试证:
。(1)试证: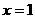 是函数
是函数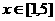 时,
时,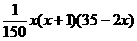 (x∈N
(x∈N 且x≤12).(1)写出明年第x个月的需求g(x)(万件)与月份x的函数关系式,并求出哪个月份的需求量超过1.4万件;(2)如果将该商品每月都投放市场P万件,要保证每月都满足供应,P应至少为多少万件?
且x≤12).(1)写出明年第x个月的需求g(x)(万件)与月份x的函数关系式,并求出哪个月份的需求量超过1.4万件;(2)如果将该商品每月都投放市场P万件,要保证每月都满足供应,P应至少为多少万件?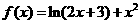 。(Ⅰ)讨论
。(Ⅰ)讨论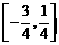 的最大值和最小值.
的最大值和最小值.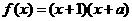 为偶函数,则
为偶函数,则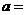 .
.  的单调递增区间是 .
的单调递增区间是 .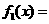
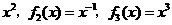 ,则
,则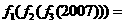 .
.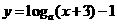
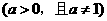 的图象恒过定点
的图象恒过定点 ,若点
,若点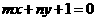 上,其中
上,其中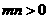 ,则
,则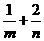 的最小值为
.
的最小值为
.