0 51528 51536 51542 51546 51552 51554 51558 51564 51566 51572 51578 51582 51584 51588 51594 51596 51602 51606 51608 51612 51614 51618 51620 51622 51623 51624 51626 51627 51628 51630 51632 51636 51638 51642 51644 51648 51654 51656 51662 51666 51668 51672 51678 51684 51686 51692 51696 51698 51704 51708 51714 51722 447348
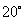 的方向,由A出发的一条公路走向是南偏东
的方向,由A出发的一条公路走向是南偏东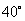 ,在B处测得公路上距B31km的C处有一人正沿公路向A城走去,走了20km之后到达D处,此时B,D间的距离为21km。这个人要走多少路才能到达A城?
,在B处测得公路上距B31km的C处有一人正沿公路向A城走去,走了20km之后到达D处,此时B,D间的距离为21km。这个人要走多少路才能到达A城?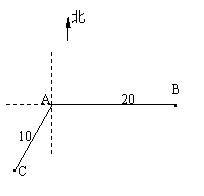 相距20海里的B处有一艘渔船遇险等待营救.甲船
相距20海里的B处有一艘渔船遇险等待营救.甲船 ,
,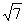
 ,
,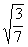 ,
,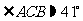 .
.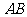 时,可以选与塔底
时,可以选与塔底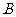 在同一水平面内的两个测点
在同一水平面内的两个测点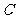 与
与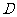 .现测得
.现测得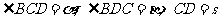 ,并在点
,并在点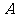 的仰角为
的仰角为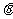 ,求塔高
,求塔高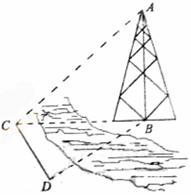
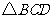 中,
中,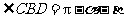 .
.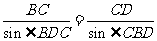 .
.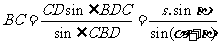 .
.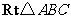 中,
中,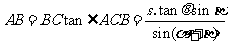 .
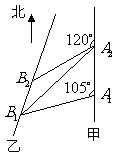
.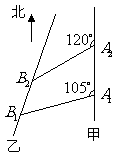 如图,甲船以每小时
如图,甲船以每小时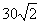 海里的速度向正北方航行,乙船按固定方向匀速直线航行,当甲船位于
海里的速度向正北方航行,乙船按固定方向匀速直线航行,当甲船位于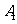 处时,乙船位于甲船的北偏西
处时,乙船位于甲船的北偏西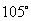 方向的
方向的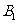 处,此时两船相距
处,此时两船相距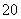 海里,当甲船航行
海里,当甲船航行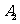 处时,乙船航行到甲船的北偏西
处时,乙船航行到甲船的北偏西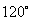 方向的
方向的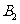 处,此时两船相距
处,此时两船相距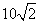 海里,问乙船每小时航行多少海里?
海里,问乙船每小时航行多少海里?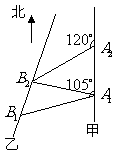 解法一:如图,连结
解法一:如图,连结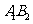 ,由已知
,由已知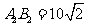 ,
,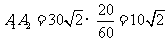 ,
,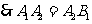 ,
,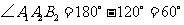 ,
,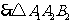 是等边三角形,
是等边三角形,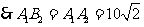 ,
,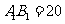 ,
,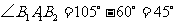 ,
,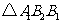 中,由余弦定理,得:
中,由余弦定理,得: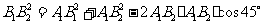
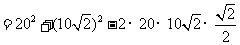
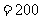 .
.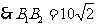 .
.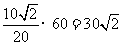 (海里/小时).
(海里/小时).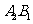 ,由已知
,由已知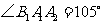 ,
,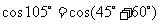
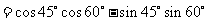
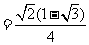 ,
,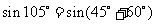
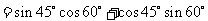
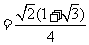 .
.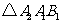 中,由余弦定理,
中,由余弦定理,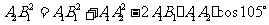
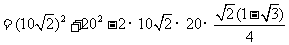
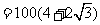 .
.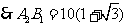 .
.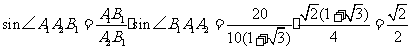 ,
,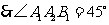 ,即
,即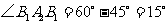 ,
,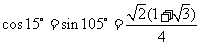 .
.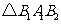 中,由已知
中,由已知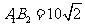 ,由余弦定理,得:
,由余弦定理,得: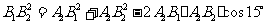
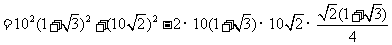

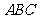 中,
中,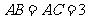 ,
,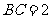 ,
,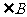 的平分线交过点
的平分线交过点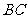 平行的线于点
平行的线于点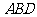 的面积.
的面积.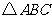 的周长为
的周长为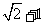 ,且
,且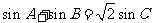 .
.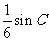 ,求角
,求角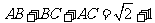 ,
,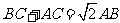 ,
,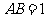 .
.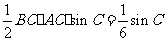 ,得
,得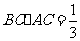 ,
,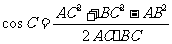
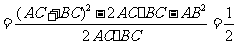 ,
,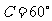 .
.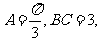 则△ABC的周长为( ).
则△ABC的周长为( ).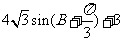 B.
B.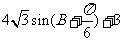
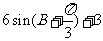 D.
D.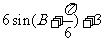
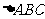 中,由正弦定理得:
中,由正弦定理得: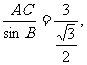 化简得:AC=
化简得:AC=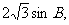
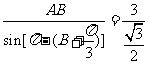 ,化简得:AB=
,化简得:AB=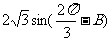 ,
,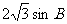 +
+
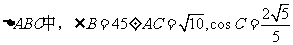 ,求(1)
,求(1)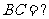 (2)若点
(2)若点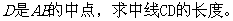
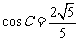 得:
得: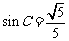
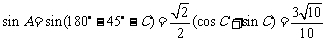 ,
,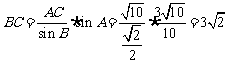 ,
,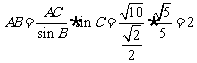 ,
,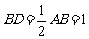
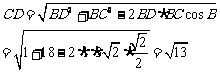
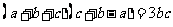 ,则
,则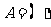 .
.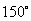 B.
B.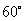 D.
D. 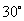
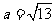 ,
,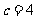 ,
,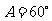 ,则
,则 __________.
__________.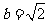 ,
,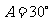 ,
,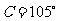 ,则此三角形的周长为__________.
,则此三角形的周长为__________.
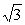 ,求c的长度.
,求c的长度.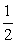 absinC,∴sinC=
absinC,∴sinC=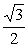 ,于是∠C=60°或∠C=120°
,于是∠C=60°或∠C=120°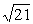
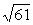
 在区间(m,m+1)内有且只有两个不等的实根?若存在,求出所有m的值;若不存在,说明理由。
在区间(m,m+1)内有且只有两个不等的实根?若存在,求出所有m的值;若不存在,说明理由。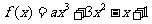 ,
, .
.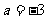 时,求证:
时,求证: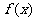 在
在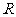 上是减函数;
上是减函数; 不等式
不等式 恒成立,求实数
恒成立,求实数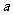 的取值范围.
的取值范围.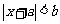 的解集是
的解集是 ,求不等式
,求不等式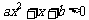 的解集.
的解集.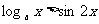 对于区间
对于区间 内的任意x都成立,则实数a的取值范围是____________
内的任意x都成立,则实数a的取值范围是____________ ,函数
,函数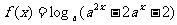 ,则使
,则使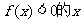 取值范围是____________
取值范围是____________