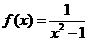3.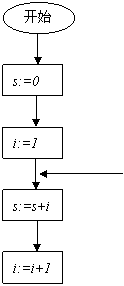 (北师大版第108页练习1 2)
(北师大版第108页练习1 2)
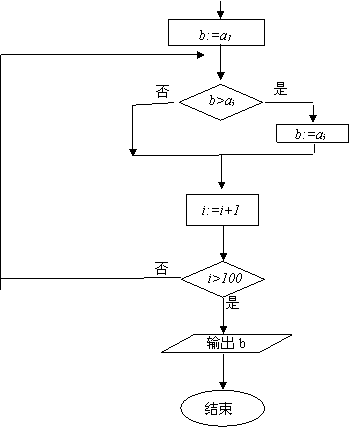
请观察给出的流程图,这是一个求和的算法的流程图,请运行几步看一看,指出该循环结构的循环体,循环变量和循环体的终止条件
|
|



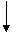

|

解:循环体是 s:=s+i
循环变量是 i
终止条件是 i>4
变式1: 观察给出的流程图,写出输出结果__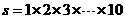 _____
_____
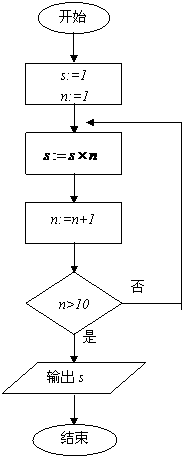
2.(北师大版第100页例3)
设计一个算法,从5个不同的数中找出最大数
变式1:写出“从5个不同数中找出最小数”的一个算法流程
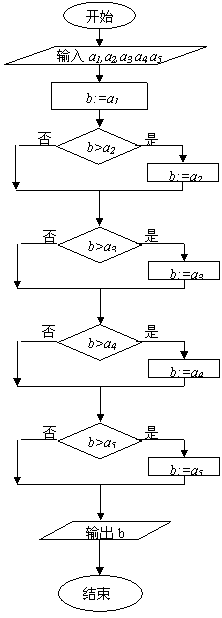 解:
解:
变式2:写出“从100个不同数中找出最小数”的一个算法流程
解:

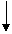
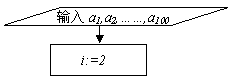
3.(人教A版选修2-3第36页例2)
(1)求 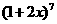 的展开式的第
4 项的系数 ;
的展开式的第
4 项的系数 ;
(2)求 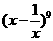 的展开式中
的展开式中 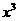 的系数 ?
的系数 ?
变式1:在二项式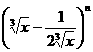 的展开式中,前三项系数的绝对值成等差数列.
的展开式中,前三项系数的绝对值成等差数列.
(1)求展开式的第四项;
(2)求展开式的常数项;
(3)求展开式的各项系数的和.
[分析]:本题旨在训练二项式定理通项公式的运用.
[解答]第一项系数的绝对值为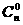 ,第二项系数的绝对值为
,第二项系数的绝对值为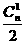 ,第三项系数的绝对值为
,第三项系数的绝对值为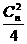 ,
,
依题意有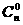 +
+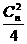 =
=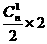 ,解得n=8,
,解得n=8,
(1)第四项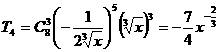 ;
;
(2)通项公式为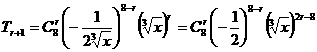 ,展开式的常数项有2r-8=0,即r=4,
,展开式的常数项有2r-8=0,即r=4,
常数项为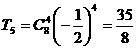 ;
;
(3)令x=1,得展开式的各项系数的和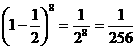 .
.
[点评]本题旨在训练二项式定理通项公式的运用,但要注意通项为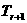 而不是
而不是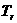 ,这是同学们最容易出错的地方.
,这是同学们最容易出错的地方.
变式2:设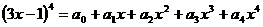 .
.
(1)求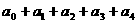 ;
;
(2)求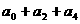 ;
;
(3)求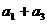 ;
;
(4)求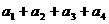 ;
;
(5)求各项二项式系数的和.
[分析]:本题旨在训练二项展开式各项的系数与二项式系数.
[解答](1)令x=1得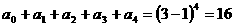 ;
;
(2)令x=-1得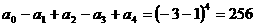 ,
,
而由(1)知: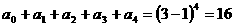 ,
,
两式相加得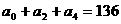 ;
;
(3)将(2)中的两式相减得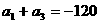 ;
;
(4)令x=0得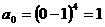 ,得
,得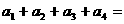
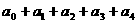 -
-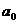 =16-1=15;
=16-1=15;
(5)各项二项式系数的和为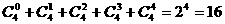 .
.
[点评]①要注意二项展开式各项的系数与二项式系数是不同的两个概念;②系数和与二项式系数和不一定相同,本题的(1)与(5)结果相同纯属巧合;③注意求系数和上述是最一般的方法,一定要理解.
变式3:二项展开式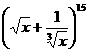 中,有理项的项数是(
)
中,有理项的项数是(
)
|
(A) 3 |
(B) 4 |
(C) 5 |
(D) 6 |
[解析]: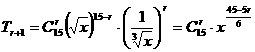 (r = 0,1,2,…,14 ),
(r = 0,1,2,…,14 ),
当r = 3,9,15时,为有理项.
[答案]:A
变式4: 若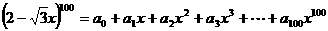 ,
,
求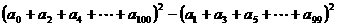 的值.
的值.
[解析]:令x=1得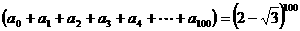 ,
,
令x=-1得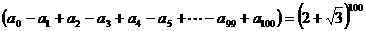
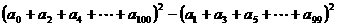
=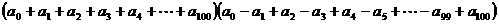
=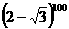
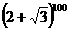
=1
[答案]:1
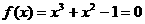 在[0,1]上的近似解,精度为0.01
在[0,1]上的近似解,精度为0.01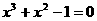 在[0,1]上的近似解,若f(0)=-1,f(0.5)=-0.125,f(1)=1则解可能在区间__[0.5,1]____
在[0,1]上的近似解,若f(0)=-1,f(0.5)=-0.125,f(1)=1则解可能在区间__[0.5,1]____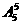 种方法;
种方法; 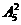 种方法;
种方法; 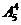 种方法;
种方法; 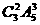 种方法;
种方法; 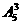 种方法;
种方法; 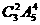 种方法;
种方法;  因此,共有不同的出牌方法
因此,共有不同的出牌方法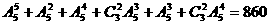 种.
种.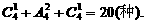 ∴分三类,共有分法
∴分三类,共有分法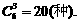 故共有分法
故共有分法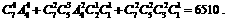
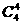 种 2)取3个红球1个白球,有
种 2)取3个红球1个白球,有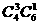 种;3)取2个红球2个白球,有
种;3)取2个红球2个白球,有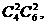

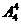 =288,解得10+x=12.
=288,解得10+x=12.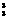 -1种;次位排4、5时有2 A
-1种;次位排4、5时有2 A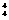 种,共计24种;
种,共计24种;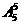 =120种;
=120种;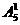 种取法,其余3个数位可以从余下的5个数字(包括0)中任取3个排列,所以可以组成
种取法,其余3个数位可以从余下的5个数字(包括0)中任取3个排列,所以可以组成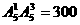 个四位数;
个四位数;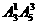 个,无数字0的有
个,无数字0的有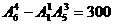 个四位数;
个四位数;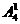 种排法,由于0不能放在首位,因此首位数字只能有
种排法,由于0不能放在首位,因此首位数字只能有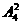 ,所以共有
,所以共有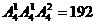 个四位奇数;
个四位奇数;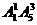 个四位偶数;2在个位时,有
个四位偶数;2在个位时,有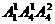 个四位偶数,所以共有
个四位偶数,所以共有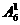 =6个;
=6个;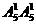 =25个;
=25个;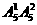 =100个;
=100个;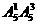 =300个;
=300个;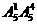 =600个;
=600个;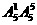 =600个;
=600个;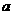 ,
,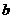 ,都有
,都有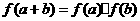 ”的函数例子.
”的函数例子.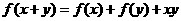 ,
,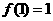 ,则f(25)= ___________________.
,则f(25)= ___________________.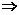
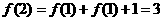
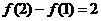
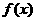 是定义在R上的偶函数,其图象关于直线
是定义在R上的偶函数,其图象关于直线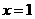 对称,对任意
对称,对任意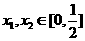 ,都有
,都有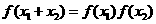
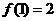 ,求
,求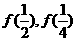
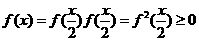 , x∈[0,1].
, x∈[0,1].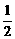 )·f(
)·f(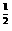 .
.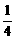 )·f(
)·f(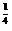 .
.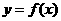 关于直线x=1对称,故f(x)=f(1+1-x)
关于直线x=1对称,故f(x)=f(1+1-x) f(x)=f(2-x),x∈R.
f(x)=f(2-x),x∈R.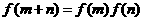 且当
且当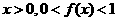
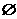 ,求a的取值范围.
,求a的取值范围.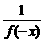 >1.
>1.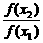 <1.∴f(x2)<f(x1).
<1.∴f(x2)<f(x1).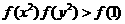
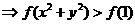
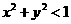
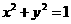 相离或相切。
相离或相切。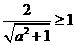
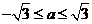
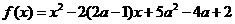 在区间[0,1]上的最小值
在区间[0,1]上的最小值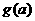 的表达式.
的表达式.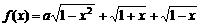 的最大值为g(a).
的最大值为g(a).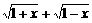 ,求t的取值范围,并把f(x)表示为t的函数m(t)
,求t的取值范围,并把f(x)表示为t的函数m(t)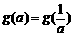 的所有实数a
的所有实数a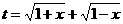 ,
,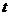 有意义,必须
有意义,必须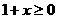 且
且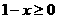 ,即
,即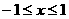
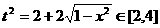 ,且
,且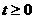 ……① ∴
……① ∴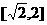 。
。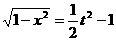 ,∴
,∴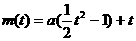
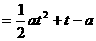 ,
,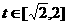 。
。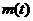
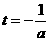 是抛物线
是抛物线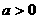 时,函数
时,函数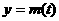 ,
,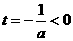 知
知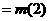
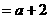 ;
;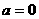 时,
时,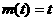 ,
,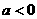 时,,函数
时,,函数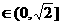 即
即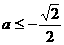 时,
时,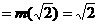 ,
,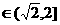 即
即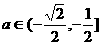 时,
时,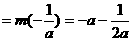 ,
,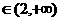 即
即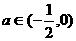 时,
时,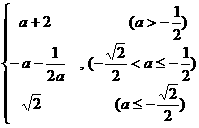 。
。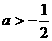 时,
时,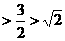 ;
;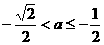 时,
时,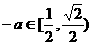 ,
,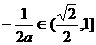 ,∴
,∴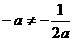 ,
,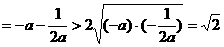 ,故当
,故当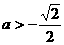 时,
时,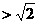 ;
;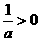 ,由
,由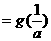 知:
知: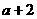
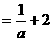 ,故
,故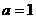 ;
;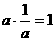 ,故
,故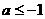 或
或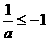 ,从而有
,从而有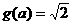 或
或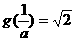 ,
,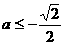 ,
,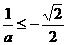 ,即
,即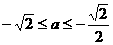 ,
,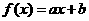 ,则
,则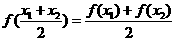
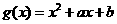 ,则
,则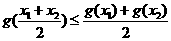
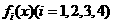 是定义在[0,1]上的四个函数,其中满足性质:“对[0,1]中任意的
是定义在[0,1]上的四个函数,其中满足性质:“对[0,1]中任意的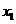 和
和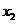 ,任意
,任意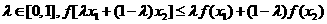 恒成立”的只有 ( )
恒成立”的只有 ( )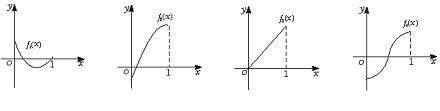
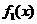
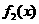
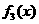
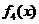
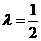 时,符合条件的函数是凹函数,从图像可看出有
时,符合条件的函数是凹函数,从图像可看出有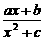 的图象如下图所示,则a、b、c的大小关系是
的图象如下图所示,则a、b、c的大小关系是 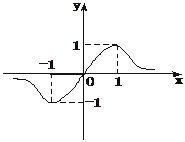
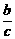 =0,∴b=0.f(1)=1,∴
=0,∴b=0.f(1)=1,∴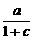 =1.
=1.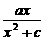 >0,
>0,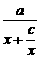 ,
,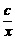 ≥2
≥2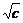 ,
,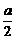 =1.∴a=2.
=1.∴a=2.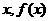 表示弧AB与弦AB
表示弧AB与弦AB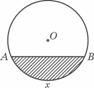 所围成的弓形面积的2倍,则函数
所围成的弓形面积的2倍,则函数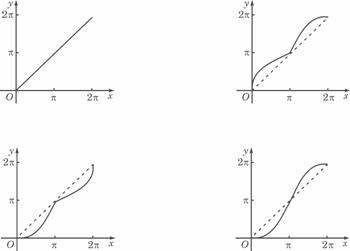
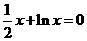 (2)
(2)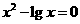
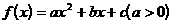 ,方程
,方程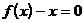 的两个根
的两个根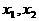 满足
满足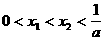 . 当
. 当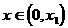 时,证明
时,证明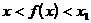 .
.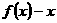 的表达式,从而得到函数
的表达式,从而得到函数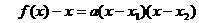 .
.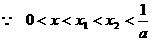 ,
,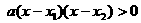 ,
,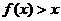 .
.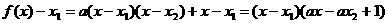 ,
,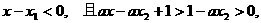
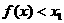 ,
,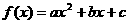 .
.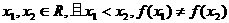 ,方程
,方程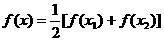 有2个不等实根,
有2个不等实根,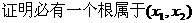
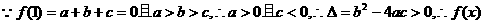
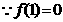 ,∴1是
,∴1是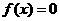 的一个根,由韦达定理知另一根为
的一个根,由韦达定理知另一根为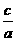 ,
,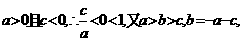
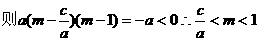
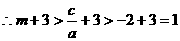
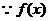 在(1,+∞)单调递增,
在(1,+∞)单调递增,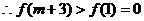 ,即存在这样的m使
,即存在这样的m使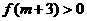
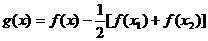 ,则
,则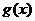 是二次函数.
是二次函数.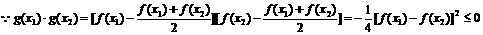
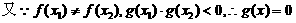 有两个不等实根,且方程
有两个不等实根,且方程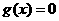 的根必有一个属于
的根必有一个属于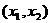 .
.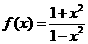 ,求证:(1)
,求证:(1)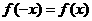 (2)
(2)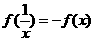
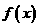 对于任意实数
对于任意实数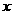 满足条件
满足条件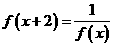 ,若
,若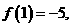 则
则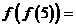 __________.
__________.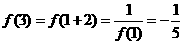 ,
,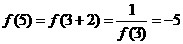 ,又
,又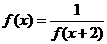 ,
,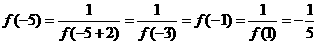
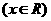 满足
满足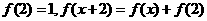 ,则
,则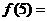
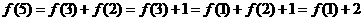 ,令
,令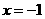 ,则
,则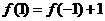 ,又∵
,又∵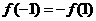 ,
,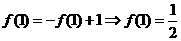 ,∴
,∴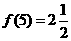
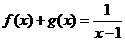 ,则
,则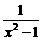 B.
B.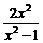 C.
C.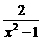 D.
D.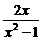
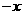 代
代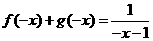 ,即
,即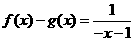 ②
②