Ⅰ.运用函数与方程、表达式相互转化的观点解决函数、方程、表达式问题。
例1 已知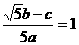 ,(a、b、c∈R),则有( )
,(a、b、c∈R),则有( )
(A)  (B)
(B) 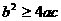 (C)
(C) 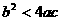 (D)
(D) 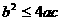
解析 法一:依题设有 a·5-b·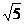 +c=0
+c=0
∴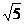 是实系数一元二次方程
是实系数一元二次方程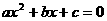 的一个实根;
的一个实根;
∴△= ≥0 ∴
≥0 ∴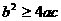 故选(B)
故选(B)
法二:去分母,移项,两边平方得:
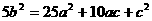 ≥10ac+2·5a·c=20ac
≥10ac+2·5a·c=20ac
∴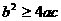 故选(B)
故选(B)
点评解法一通过简单转化,敏锐地抓住了数与式的特点,运用方程的思想使问题得到解决;解法二转化为b2是a、c的函数,运用重要不等式,思路清晰,水到渠成。
练习1 已知关于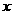 的方程
的方程 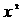 -(2 m-8)x +
-(2 m-8)x +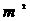 -16 = 0的两个实根
-16 = 0的两个实根 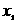 、
、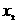 满足
满足 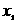 <
<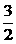 <
<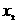 ,则实数m的取值范围_______________。
,则实数m的取值范围_______________。
答案: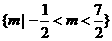 ;
;
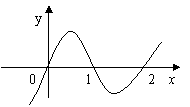 2 已知函数
2 已知函数 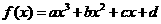 的图象如下,则( )
的图象如下,则( )
(A)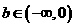 (B)
(B)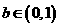
(C) 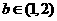 (D)
(D)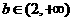
答案:A.
3 求使不等式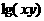 ≤
≤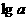 ·
·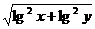 对大于1的任意x、y恒成立的a的取值范围。
对大于1的任意x、y恒成立的a的取值范围。
Ⅱ:构造函数或方程解决有关问题:
例2 已知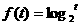 ,t∈[
,t∈[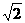 ,8],对于f(t)值域内的所有实数m,不等式
,8],对于f(t)值域内的所有实数m,不等式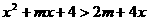 恒成立,求x的取值范围。
恒成立,求x的取值范围。
解析∵t∈[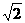 ,8],∴f(t)∈[
,8],∴f(t)∈[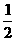 ,3]
,3]
原题转化为: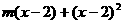 >0恒成立,为m的一次函数(这里思维的转化很重要)
>0恒成立,为m的一次函数(这里思维的转化很重要)
当x=2时,不等式不成立。
∴x≠2。令g(m)=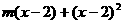 ,m∈[
,m∈[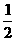 ,3]
,3]
问题转化为g(m)在m∈[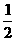 ,3]上恒对于0,则:
,3]上恒对于0,则: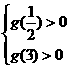 ;
;
解得:x>2或x<-1
评析 首先明确本题是求x的取值范围,这里注意另一个变量m,不等式的左边恰是m的一次函数,因此依据一次函数的特性得到解决。在多个字母变量的问题中,选准“主元”往往是解题的关键。
例3 为了更好的了解鲸的生活习性,某动物保护组织在受伤的鲸身上装了电子监测装置,从海洋放归点A处,如图(1)所示,把它放回大海,并沿海岸线由西向东不停地对它进行了长达40分钟的跟踪观测,每隔10分钟踩点测得数据如下表(设鲸沿海面游动),然后又在观测站B处对鲸进行生活习性的详细观测,已知AB=15km,观测站B的观测半径为5km。
|
观测时刻 t(分钟) |
跟踪观测点到放归 点的距离a(km) |
鲸位于跟踪观测点正北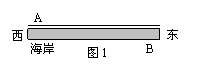 方向的距离b(km) 方向的距离b(km) |
|
10 |
1 |
0.999 |
|
20 |
2 |
1.413 |
|
30 |
3 |
1.732 |
|
40 |
4 |
2.001 |
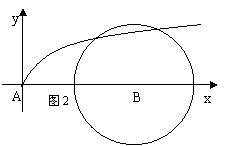
(1)据表中信息:①计算出鲸沿海岸线方向运动的速度;②试写出a、b近似地满足的关系式并
画出鲸的运动路线草图;
 (2)若鲸继续以(1)-②运动的路线运动,试预测,该鲸经过多长时间(从放归时开设计时)可进入前方观测站B的观测范围?并求出可持续观测的时间及最佳观测时刻。(注:
(2)若鲸继续以(1)-②运动的路线运动,试预测,该鲸经过多长时间(从放归时开设计时)可进入前方观测站B的观测范围?并求出可持续观测的时间及最佳观测时刻。(注: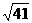 ≈6.40;精确到1分钟)
≈6.40;精确到1分钟)
解析(1)由表中的信息可知:
①鲸沿海岸线方向运动的速度为: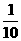 (km/分钟)
(km/分钟)
②a、b近似地满足的关系式为: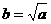 运动路线如图
运动路线如图
(2)以A为原点,海岸线AB为x轴建立直角坐标系,设鲸所在
位置点P(x,y),由①、②得: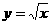 ,又B(15,0),
,又B(15,0),
依题意:观测站B的观测范围是:
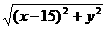 ≤5 (y≥0) 又
≤5 (y≥0) 又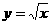
∴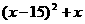 ≤25 解得:11.30≤x≤17.70
≤25 解得:11.30≤x≤17.70
由①得:∴该鲸经过t=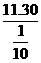 =113分钟可进入前方观测站B的观测范围
=113分钟可进入前方观测站B的观测范围
持续时间: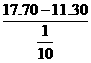 =64分钟
=64分钟
∴该鲸与B站的距离d=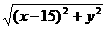 =
=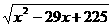
当d最小时为最佳观测时刻,这时x=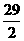 =14.5,t=145分钟。
=14.5,t=145分钟。
练习4.已知关于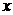 的方程
的方程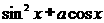 -2
-2 = 0有实数解,求实数
= 0有实数解,求实数 的取值范围。
的取值范围。
(答案:0≤ ≤4-
≤4-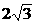 )
)
Ⅲ:运用函数与方程的思想解决数列问题
例4设等差数列{an}的前n项和为Sn,已知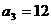 ,
,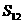 >0,
>0,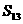 <0,
<0,
(1)求公差d的取值范围;
(2)指出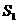 、
、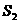 、
、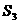 …,
…,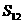 中哪一个最大,并说明理由。
中哪一个最大,并说明理由。
解析(1)由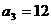 得:
得: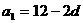 ,
,
∵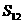 =
=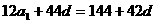 >0
>0 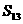 =
=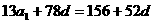 <0
<0
∴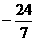 <d<-3
<d<-3
(2)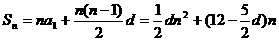
∵d<0,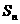 是关于n 的二次函数,对称轴方程为:x=
是关于n 的二次函数,对称轴方程为:x=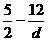
∵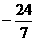 <d<-3 ∴6<
<d<-3 ∴6<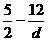 <
<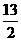 ∴当n=6时,
∴当n=6时,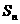 最大。
最大。
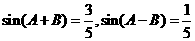 。
。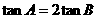 ;
; ,求AB边上的高。
,求AB边上的高。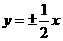 ,则该双曲线的离心率
,则该双曲线的离心率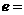 ( )
( )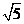 C
C 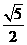 D
D 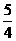
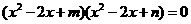 的四个根组成一个首项为
的四个根组成一个首项为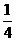 的等差数列,则
的等差数列,则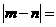 (
)
(
)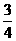 C
C 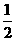 D
D 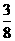
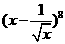 展开式中
展开式中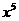 的系数为____________.
的系数为____________.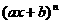 (n∈N*)与二项式定理是密切相关的,利用这个函数用赋值法和比较系数法可以解决很多二项式定理的问题。
(n∈N*)与二项式定理是密切相关的,利用这个函数用赋值法和比较系数法可以解决很多二项式定理的问题。