相位变换-φ>0左移;φ<0右移;
周期变换- ω>1,横坐标缩短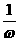 倍;0< ω<1,横坐标伸长
倍;0< ω<1,横坐标伸长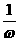 倍;
倍;
振幅变换-A>1,纵坐标伸长A倍;0<A<1,纵坐标缩短A倍
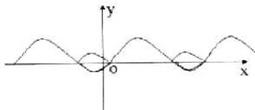
练习:已知:如图是函数y=2sin(ωx+φ) 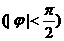 的图象,那么
的图象,那么
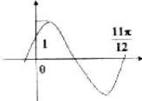
A.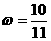 ,
,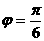 ;
;
B.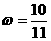 ,
,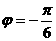 ;
;
C.ω=2,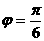 ;
;
D.ω=2,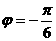 ;
;
例1.用五点法作函数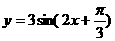 的简图,并说明它是通过y=sinx的图象作怎样的变换得到的。
的简图,并说明它是通过y=sinx的图象作怎样的变换得到的。
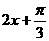 |
0 |
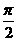 |
π |
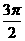 |
2π |
|
x |
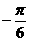 |
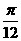 |
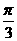 |
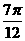 |
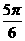 |
|
y |
0 |
3 |
0 |
-3 |
0 |
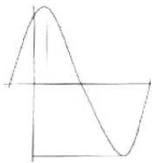
先将y=sinx(向左平移)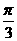 个单位,再把所得的各点(横坐标缩短)到原来的(1/2),(纵坐标伸长)到原来的(3)而得到的。
个单位,再把所得的各点(横坐标缩短)到原来的(1/2),(纵坐标伸长)到原来的(3)而得到的。
先将y=sinx图象的各点的(横坐标缩短到原来的1/2)倍,再把各点向(左)平移(π/6)个单位,然后把所得的各点的(纵坐标伸长)到原来的(3)而得到的。
例2.函数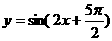 的图像的一条对称轴
的图像的一条对称轴
方程是()。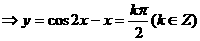
A.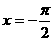
B.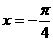
C.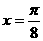
D.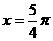
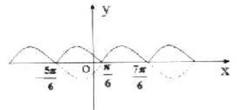
例3.函数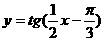 在一个周期内的图象是()
在一个周期内的图象是()
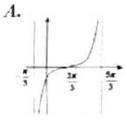
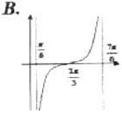
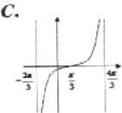
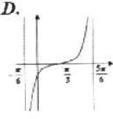
例4.如图,已知正弦函数y=Asin(ωx+φ)(A>0)的一个周期的图象,试求函数y的解析表达式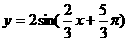
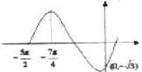
例5.已知函数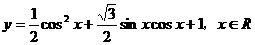 ,
,
(1)当y取得最大值时,求自变量x的集合;
(2)该函数的图象可由y=sinx(x∈R)的图象经过怎样的平移和伸缩变换得到(2000年高考,难度0.70)
(1)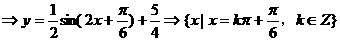
(2)
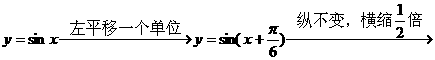


例6.求下列各方程在区间[0,2π]内实数解的个数
(1)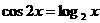 ;
;
(2)sinx=sin4x;
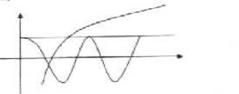
(1)一个实解
(2)九个实解
例7 已知函数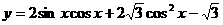
(1)作出它的简图:
(2)填空回答问题:
〈1〉振幅 2 ;
〈2〉周期 π ;
〈3〉频率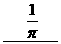 ;
;
〈4〉相位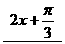 ;
;
〈5〉初相 ;
;
〈6〉定义域 R ;
〈7〉值域 [-2,2] ;
〈8〉当x=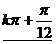 时
时 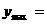 2 ;
2 ;
当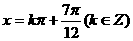 时,
时, -2 ;
-2 ;
〈9〉单调递增区间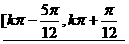 k∈Z。;
k∈Z。;
单调递减区间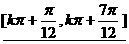 k∈Z。
k∈Z。
〈10〉当x∈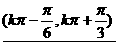 k∈Z时,y>0
k∈Z时,y>0
当x∈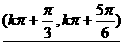 k∈Z时,y<0
k∈Z时,y<0
〈11〉图象的对称轴方程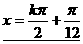 k∈Z。
k∈Z。
〈12〉图像的对称中心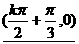 k∈Z。
k∈Z。
作业:
1.已知函数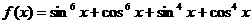
求(1)f(x)的值域
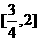
(2)f(x)的最小正周期
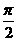
(3)f(x)的单调区间
单调递增区间为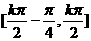 k∈Z。
k∈Z。
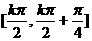 k∈Z。
k∈Z。
|
|
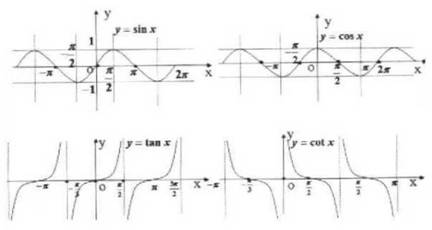
y=sinx |
y=cosx |
y=tanx |
y=cotx |
|
定义域 |
R |
R |
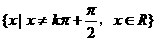 |
{x|x≠kπ, x∈R} |
|
值域 |
[-1,1] |
[-1,1] |
R |
R |
|
周期性 |
最小正周期2π |
最小正周期2π |
最小正周期π |
最小正周期π |
|
单调区间 k∈z |
增区间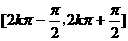 减区间 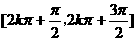 |
增区间 [2kπ-π,2kπ] 减区间 [2kπ,2kπ+π] |
增区间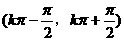 |
减区间 (kπ,kπ+π) |
|
最值点 k∈z |
最大值点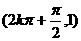 最小值点 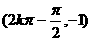 |
最大值点 (2kπ,1) 最小值点 (2kπ+π,-1) |
无 |
无 |
|
对称中心 k∈z |
(kπ,0) |
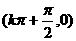 |
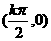 |
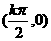 |
|
对称轴 k∈z |
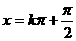 |
x=kπ |
无 |
无 |
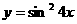 (
(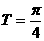 )
)
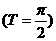
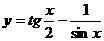 (T=π)
(T=π)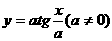 (T=|a|π)
(T=|a|π)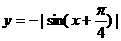 的单调区间
的单调区间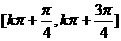 k∈Z。
k∈Z。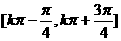 k∈Z。
k∈Z。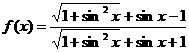 (奇)
(奇)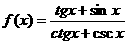 (偶)
(偶)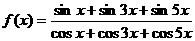 (奇)
(奇)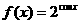 (偶)
(偶)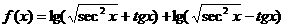 (偶)
(偶)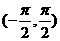 递增。
递增。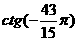 和
和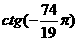
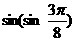 和
和 ;
;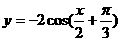 ;
;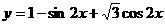 (减区间)
(减区间)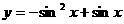 ;
;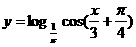 (增区间)
(增区间)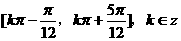
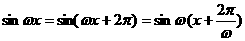 ,
,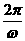 。
。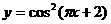 ;(1)T=1;
;(1)T=1;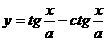 ;(2)
;(2)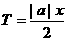 ;
;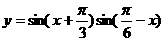 ;(3)T=π;
;(3)T=π;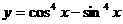 ;(4)T=π;
;(4)T=π;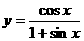 ;(5)T=2π;
;(5)T=2π;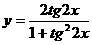 ;(6)
;(6)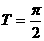 ;
;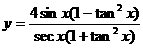 的周期。
的周期。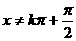 ,k∈z}
,k∈z}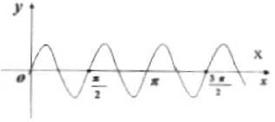
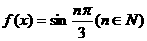 ,
,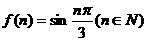 的周期为6
的周期为6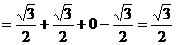
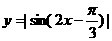
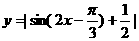
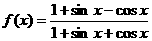 ;非奇非偶函数 既奇又偶函数
;非奇非偶函数 既奇又偶函数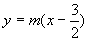 是过定点(
是过定点(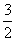 ,0)的直线系.
3.A、 提示:由图象知f(x)=0的三个实根是0,1,2这样,函数解析式可变形f(x)=ax(x-1)(x-2),又从图象中可以看出当x∈(0,1)∪(2,+∞)时,f(x)>0.而当x>2时,x,(x-1),(x-2)均大于0,所以a>0,而
,0)的直线系.
3.A、 提示:由图象知f(x)=0的三个实根是0,1,2这样,函数解析式可变形f(x)=ax(x-1)(x-2),又从图象中可以看出当x∈(0,1)∪(2,+∞)时,f(x)>0.而当x>2时,x,(x-1),(x-2)均大于0,所以a>0,而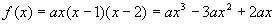 可知b=-3a<0,故选(A)
4.A
5.A
6.(可以利用图象法求解)
(1)x≤-1或0<x≤3 (2)x≤-1
7.1
8.210°
9.
10.A
11.D 提示:在曲线方程中,分x≥0或x<0两种情形讨论,作出图形即可.
12.C
13.
可知b=-3a<0,故选(A)
4.A
5.A
6.(可以利用图象法求解)
(1)x≤-1或0<x≤3 (2)x≤-1
7.1
8.210°
9.
10.A
11.D 提示:在曲线方程中,分x≥0或x<0两种情形讨论,作出图形即可.
12.C
13.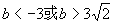 14.A 提示:f(x)可以视作:A(cosx,sinx),B(1,2),则f(x)=kAB,而A点为圆x2+y2=1上的动点
14.A 提示:f(x)可以视作:A(cosx,sinx),B(1,2),则f(x)=kAB,而A点为圆x2+y2=1上的动点