2.几何应用题.
例11.如右图,设田地喷灌水管AB高出地面1.5米,在B处有一个自动旋转的喷水头,一瞬间,喷出水流是抛物线状,喷头B与水流最高点C的连线与水平地面成45°角,若C比B高出2米,在所建的坐标系中,求水流的落地点D到点A的距离是多少米?
分析:本题要构造解析几何模型,其关键是确定抛物线的方程.
解. 依题可知.BE=CE=2(米),CF=CE+EF=3.5(米),点B的坐标为(0,1.5)
∴抛物线的方程为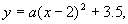 由于它经过点B,故
由于它经过点B,故
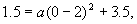 ∴4a=–2, ∴
∴4a=–2, ∴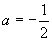 .
故抛物线的方程为
.
故抛物线的方程为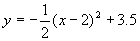 当y=0时,
当y=0时,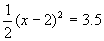 ∴
∴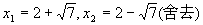 即水流落地点D和点A的距离为
即水流落地点D和点A的距离为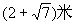 例7.如右图是抛物线型拱桥,设水面宽AB=18米,拱项离水面的距离为8米,一货船在水面上的部分的横断面为一矩形CDEF.
(1)若矩形的长CD=9米,那么矩形的高DE不能超过多少米才能使船通过拱桥?
(2)求矩形面积S的“临界值”M:即当S≤M时,适当调整矩形的长和高,船能通过拱桥;而当S>M时,无论怎样调整矩形的长和高,船都不能通过拱桥.
分析:本题确切指明是抛物线型,因此关键是确定抛物线段的方程.
解:(1)如图,以O点为原点,过O平行AB的直线为x轴以线段AB的垂直平分线为y轴建立直角坐标系.则B(9,-8)
例7.如右图是抛物线型拱桥,设水面宽AB=18米,拱项离水面的距离为8米,一货船在水面上的部分的横断面为一矩形CDEF.
(1)若矩形的长CD=9米,那么矩形的高DE不能超过多少米才能使船通过拱桥?
(2)求矩形面积S的“临界值”M:即当S≤M时,适当调整矩形的长和高,船能通过拱桥;而当S>M时,无论怎样调整矩形的长和高,船都不能通过拱桥.
分析:本题确切指明是抛物线型,因此关键是确定抛物线段的方程.
解:(1)如图,以O点为原点,过O平行AB的直线为x轴以线段AB的垂直平分线为y轴建立直角坐标系.则B(9,-8)
设抛物线方程为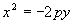 (p>0)
∵B点在抛物线上,
∴81=–2p(–8) ∴
(p>0)
∵B点在抛物线上,
∴81=–2p(–8) ∴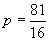 ∴抛物线的方程为
∴抛物线的方程为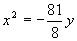 当
当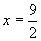 时,y=–2,∴|DE|=6,
所以当矩形的高DE不超过6米时,才能使船通过拱桥. 时,y=–2,∴|DE|=6,
所以当矩形的高DE不超过6米时,才能使船通过拱桥. |
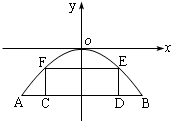 |
(2)设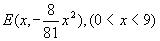 则|CD|=2x,
则|CD|=2x,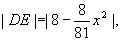 ∴
∴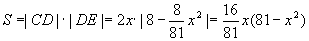
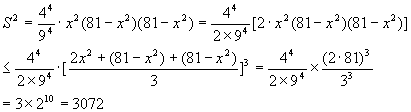 当且仅当
当且仅当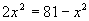 即
即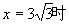 ,8取得最大值32
,8取得最大值32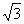 平方米,∴矩形面积S的临界值M为
平方米,∴矩形面积S的临界值M为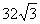 。
。
例12、如图,某隧道设计为双向四车道,车道总宽22米,要求通行车辆限高4.5米,隧道全长2.5千米,隧道的拱线近似地看成半个椭圆形状。
(1)若最大拱高h为6米,则隧道设计的拱宽l是多少?
(2)若最大拱高h不小于6米,则应如何设计拱高h和拱宽l,才能使半个椭圆形隧道的土方工程量最小?
(半个椭圆的面积公式为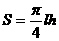 。柱体体积为:底面积乘以高。本题结果均精确到0.1米)
。柱体体积为:底面积乘以高。本题结果均精确到0.1米)
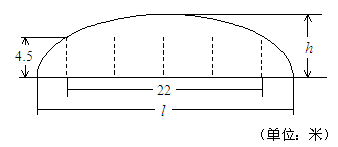
[解](1)如图建立直角坐标系,则点P(11,4.5)
椭圆方程为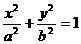
将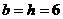 与点P坐标代入椭圆方程,得
与点P坐标代入椭圆方程,得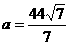 ,此时
,此时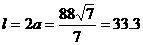
因此隧道的拱宽约为33.3米。
(2)[解一]由椭圆方程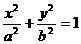
得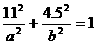
因为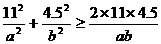 ,即
,即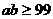 ,且
,且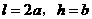
所以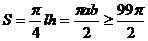
当S取最小值时,有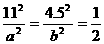 ,得
,得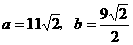
此时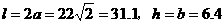
故当拱高约为6.4米,拱宽约为31.1米时,土方工程量最小
[解二]由椭圆方程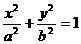 ,得
,得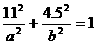
于是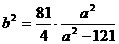
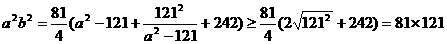
即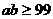 ,当S取最小值时,有
,当S取最小值时,有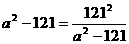
得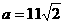 ,
,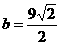 ,以下同解一
,以下同解一
例13、 2003年10月15日9时,“神舟”五号载人飞船发射升空,于9时9分50秒准确进入预定轨道,开始巡天飞行。该轨道是以地球的中心 为一个焦点的椭圆。选取坐标系如图所示,椭圆中心在原点。近地点A距地面200km,远地点B距地面350km。已知地球半径R=6371km。
为一个焦点的椭圆。选取坐标系如图所示,椭圆中心在原点。近地点A距地面200km,远地点B距地面350km。已知地球半径R=6371km。
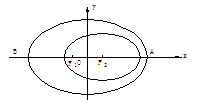 (I)求飞船飞行的椭圆轨道的方程;
(I)求飞船飞行的椭圆轨道的方程;
(II)飞船绕地球飞行了十四圈后,于16日5时59分返
回舱与推进舱分离,结束巡天飞行,飞船共巡天飞行了约
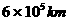 ,问飞船巡天飞行的平均速度是多少km/s?
,问飞船巡天飞行的平均速度是多少km/s?
(结果精确到1km/s)(注:km/s即千米/秒)
本小题主要考查椭圆等基本知识,考查分析问题和解决问题的能力。满分14分
解:(I)设椭圆的方程为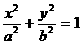 由题设条件得
由题设条件得
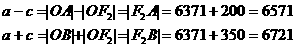
解得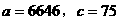 所以
所以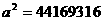
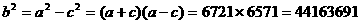
所以椭圆的方程为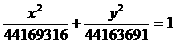
(注:由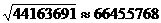 得椭圆的方程为
得椭圆的方程为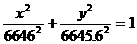 ,也是正确的。)
,也是正确的。)
(II)从15日9时到16日6时共21个小时,合21×3600秒
减去开始的9分50秒,即9×60+50=590(秒),再减去最后多计的1分钟,共减去590+60=650(秒) 得飞船巡天飞行的时间是 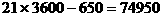 (秒)
(秒)
平均速度是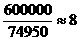 (千米/秒) 所以飞船巡天飞行的平均速度是8km/s。
(千米/秒) 所以飞船巡天飞行的平均速度是8km/s。
例14、A、B两个代表队进行乒乓球对抗赛,每队三名队员,A队队员是A1,A2,A3,B
队队员是B1,B2,B3,按以往多次比赛的统计,对阵队员之间胜负概率如下:
|
对阵队员 |
A队队员胜的概率 |
A队队员负的概率 |
|
A1对B1 |
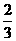 |
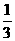 |
|
A2对B2 |
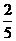 |
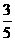 |
|
A3对B3 |
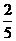 |
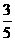 |
现按表中对阵方式出场,每场胜队得1分,负队得0分,设A队、B队最后所得总
分分别为ξ、η
(1)求ξ、η的概率分布;
(2)求Eξ,Eη.
本小题考查离散型随机变量分布列和数学期望等概念,考查运用概率知识解决实际问题的能力
解:(1)ξ、η的可能取值分别为3,2,1,0.
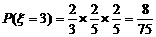
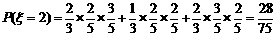
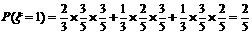 ,
,
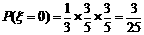
根据题意知ξ+η=3,所以 P(η=0)=P(ξ=3)=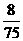 , P(η=1)=P(ξ=2)=
, P(η=1)=P(ξ=2)= 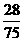
P(η=2)=P(ξ=1)= 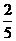 , P(η=3)=P(ξ=0)=
, P(η=3)=P(ξ=0)= 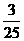 .
.
(2)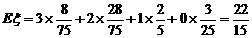 ; 因为ξ+η=3,所以
; 因为ξ+η=3,所以 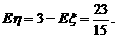
1.代数应用题
例1.在测量某物理量的过程中,因仪器和观测的误差,使得n次测量分别得到a1,a2,…an共n个数据,我们规定所测量的物理量的“最佳近似值”a是这样一个量:与其他近似值比较,a与各数据的差的平方和最小,依此规定,从a1,a2,…an推出的a=______________.
分析:本题是与其它学科相关的数学应用问题,要正确理解题意,并能把文字语言转化为符号语言.
解:依题意,本题即是求使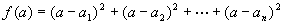 的最小值时,a的取值.
∵
的最小值时,a的取值.
∵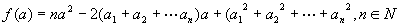 ,
故当
,
故当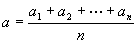 时,f(a)最小.
例2.《中华人民共和国个人所得税法》规定,公民全月工资、薪金所得不超过800元的部分不必纳锐,超过500元的部分为全月应纳税所得额,此项税款按下表分段累进计算:
时,f(a)最小.
例2.《中华人民共和国个人所得税法》规定,公民全月工资、薪金所得不超过800元的部分不必纳锐,超过500元的部分为全月应纳税所得额,此项税款按下表分段累进计算:
|
全月应纳税所得额 |
税率 |
|
不超过500元的部分 |
5% |
|
超过500元至2000元的部分 |
10% |
|
超过2000元至5000元的部分 |
15% |
某人一月份应交纳此项税款26.78元,则他的当月工资、薪金所得介于
(A)800-900元 (B)900元-1200元 (C)1200-1500元 (D)1500-2000元
分析:注意分类讨论思想的应用.
思路一:若收入1300元应纳税:500×5%=25元<26.78元
∴此人收入超过1300元,淘汰A、B.
若收入1500元应纳税:500×5%+200×10%=45元>26.78元
∴此人收入低于1500元,排除D,故选C.
思路2:设全月应纳税所得额为x元.
当x<500时,由题意知 x·5%=26.78
∴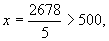 故与题意不符合.
当500<x<2000元时,则500×5%+(x–500) ×10%=26.78
∴x=517.8
∴当月工资、薪金所得额为800+517.8=1317.8元.
故选C.
例3.设计某高速公路时,要求最低车速50千米/小时,最小车距为l千米(l是定值),并且车速v与车距d之间必须满足关系
故与题意不符合.
当500<x<2000元时,则500×5%+(x–500) ×10%=26.78
∴x=517.8
∴当月工资、薪金所得额为800+517.8=1317.8元.
故选C.
例3.设计某高速公路时,要求最低车速50千米/小时,最小车距为l千米(l是定值),并且车速v与车距d之间必须满足关系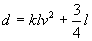 ,求:
(Ⅰ)常数k的值:
(Ⅱ)这条高速公路的一条车道上每小时的最高车流量.(单位时间车流量=车速/车距)
解:(Ⅰ)由题意,将v=50,d=l代入解析式
,求:
(Ⅰ)常数k的值:
(Ⅱ)这条高速公路的一条车道上每小时的最高车流量.(单位时间车流量=车速/车距)
解:(Ⅰ)由题意,将v=50,d=l代入解析式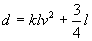 中可求得
中可求得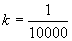 (Ⅱ)
(Ⅱ)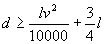 .
设每小时车流量为Q,则
.
设每小时车流量为Q,则
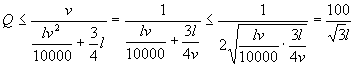 (由实际问题,
(由实际问题,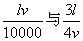 皆为正值)
当且仅当
皆为正值)
当且仅当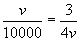 ,即
,即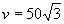 时等号成立.
而
时等号成立.
而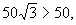 所以当车速为
所以当车速为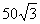 千米/小时,此高速公路一条车道上每小时的最大车流量为
千米/小时,此高速公路一条车道上每小时的最大车流量为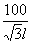 辆.
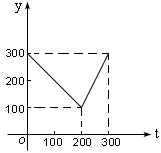
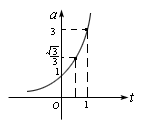
例4.某蔬菜基地种植西红柿,由历年市场行情得知,从二月一日起的300天内,西红柿市场售价与上市时间的关系用图一的一条折线表示;西红柿的种植成本与上市时间的关系用图二的抛物线表示.
辆.
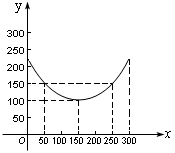
例4.某蔬菜基地种植西红柿,由历年市场行情得知,从二月一日起的300天内,西红柿市场售价与上市时间的关系用图一的一条折线表示;西红柿的种植成本与上市时间的关系用图二的抛物线表示.
 |
 |
|
图一 |
图二 |
(Ⅰ)写出图一表示的市场售价与时间的函数关系式P=f(x);写出图二表示的种植成本与时间的函数关系式Q=g(t)
(Ⅱ)认定市场售价减去种植成本为纯收益,向何时上市的西红柿纯收益最大?
(注:市场售价和种植成本的单位:元/102kg,时间单位:天)
分析:要根据函数图象正确建立函数关系式,然后求最值.
解:由图一可得市场售价与时间的函数关系为
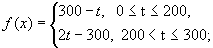 由图二可得种植成本与时间的函数关系为,
由图二可得种植成本与时间的函数关系为,
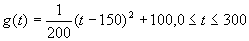 Ⅱ)设t时刻的纯收益h(t),则由题意得.
Ⅱ)设t时刻的纯收益h(t),则由题意得.
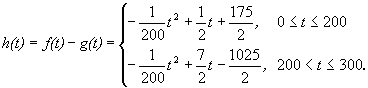 当0≤t≤200时,配方整理得
当0≤t≤200时,配方整理得
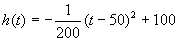 ,
∴t=50时,h(t)取得区间[0,200]上的最大值100;
当
,
∴t=50时,h(t)取得区间[0,200]上的最大值100;
当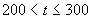 时,配方整理得,
时,配方整理得,
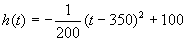 ∴当t=300时,h(t)取得区间(200,300]上的最大值87.5
综上,由100>87.5可知,h(t)在区间[0,300]上可以取得最大值100,此时t=50,即从二月一日开始的第50天时,上市的西红柿纯收益最大.
例5某企业年初有资金1000万元,如果该企业经过生产经营每年资金增长率均为50%,但每年年底都要扣除消费基金x万元,余下资金投入再生产,为实现经过5年资金达到2000万元(扣除消费资金后),那么每年扣除消费基金x应是多少万元(精确到万元)?
解:依题意,第一年年底扣除消费资金后,投入再生产资金为1000+1000×50%–x=1000×
∴当t=300时,h(t)取得区间(200,300]上的最大值87.5
综上,由100>87.5可知,h(t)在区间[0,300]上可以取得最大值100,此时t=50,即从二月一日开始的第50天时,上市的西红柿纯收益最大.
例5某企业年初有资金1000万元,如果该企业经过生产经营每年资金增长率均为50%,但每年年底都要扣除消费基金x万元,余下资金投入再生产,为实现经过5年资金达到2000万元(扣除消费资金后),那么每年扣除消费基金x应是多少万元(精确到万元)?
解:依题意,第一年年底扣除消费资金后,投入再生产资金为1000+1000×50%–x=1000×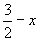 第二年投入再生产资金为
第二年投入再生产资金为
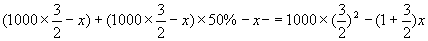 ……
……
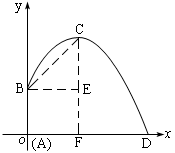 第五年投入再生产资金为
第五年投入再生产资金为
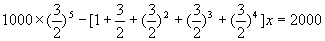 化简得:
化简得: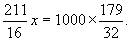 故x≈424(万元)
答:每年扣除消费资金为424元.
说明:本题关键是寻求每年投入再生产资金的规律,构造数列模型来解题.
故x≈424(万元)
答:每年扣除消费资金为424元.
说明:本题关键是寻求每年投入再生产资金的规律,构造数列模型来解题.
例6在某海滨城市附近海面有一台风,据监测,当前台风中心位于城市O(如图)的东偏南

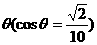 方向300km的海面P处,并以20km/h的速度向西偏北45°方向移动,台风侵袭的范围为圆形区域,当前半径为60km,并以10km/h的速度不断增大问几小时后该城市开始受到台风的侵袭?
方向300km的海面P处,并以20km/h的速度向西偏北45°方向移动,台风侵袭的范围为圆形区域,当前半径为60km,并以10km/h的速度不断增大问几小时后该城市开始受到台风的侵袭?
解:如图建立坐标系:以O为原点,正东方向为x轴正向.
在时刻:t(h)台风中心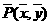 的坐标为
的坐标为
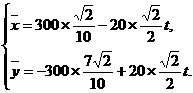
此时台风侵袭的区域是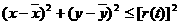 ,
,
其中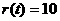 t+60,
t+60,
若在t时,该城市O受到台风的侵袭,则有
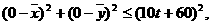
即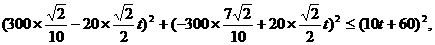
即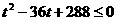 , 解得
, 解得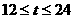 .
.
答:12小时后该城市开始受到台风气侵袭
例7、有三个新兴城镇,分别位于A,B,C三点处,且AB=AC=a,BC=2b.今计划合建一个中心医院,为同时方便三镇,准备建在BC的垂直平分线上的P点处,(建立坐标系如图)
 (Ⅰ)若希望点P到三镇距离的平方和为最小,
(Ⅰ)若希望点P到三镇距离的平方和为最小,
点P应位于何处?
(Ⅱ)若希望点P到三镇的最远距离为最小,
点P应位于何处?
本小题主要考查函数,不等式等基本知识,考查运用数学知识分析问题和解决问题的能力. (Ⅰ)解:由题设可知,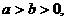 记
记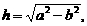 设P的坐标为(0,
设P的坐标为(0,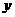 ),则P至三镇距离的平方和为
),则P至三镇距离的平方和为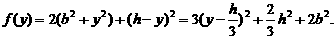 所以,当
所以,当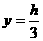 时,函数
时,函数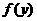 取得最小值. 答:点P的坐标是
取得最小值. 答:点P的坐标是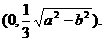
(Ⅱ)解法一:P至三镇的最远距离为 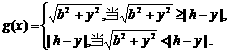
由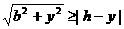 解得
解得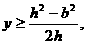 记
记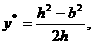 于是
于是
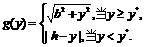 当
当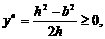 即
即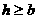 时,
时,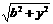 在[
在[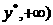 上是增函数,而
上是增函数,而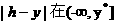 上是减函数. 由此可知,当
上是减函数. 由此可知,当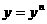 时,函数
时,函数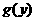 取得最小值. 当
取得最小值. 当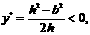 即
即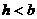 时,函数
时,函数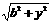 在[
在[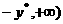 上,当
上,当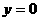 时,取得最小值
时,取得最小值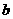 ,而
,而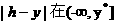 上为减函数,且
上为减函数,且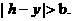 可见, 当
可见, 当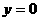 时, 函数
时, 函数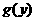 取得最小值. 答当
取得最小值. 答当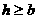 时,点P的坐标为
时,点P的坐标为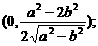 当
当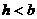 时,点P的坐标为(0,0),其中
时,点P的坐标为(0,0),其中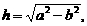
解法二:P至三镇的最远距离为 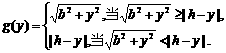 由
由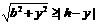 解得
解得
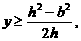 记
记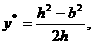 于是
于是
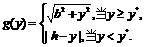
当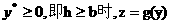 的图象如图
的图象如图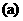 ,因此,当
,因此,当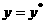 时,函数
时,函数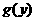 取得最小值.
取得最小值.
 当
当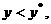 即
即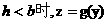 的图象如图
的图象如图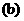 ,因此,当
,因此,当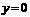 时,函数
时,函数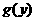 取得最小值.
取得最小值.
答:当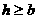 时,点P的坐标为
时,点P的坐标为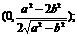 当
当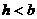 ,点P的坐标为(0,0),其中
,点P的坐标为(0,0),其中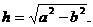
解法三:因为在△ABC中,AB=AC=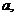 所以△ABC的外心M在射线AO上,其坐标为
所以△ABC的外心M在射线AO上,其坐标为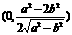 ,
,
 且AM=BM=CM. 当P在射线MA上,记P为P1;当P在射线MA的反向延长线上,记P为P2,
且AM=BM=CM. 当P在射线MA上,记P为P1;当P在射线MA的反向延长线上,记P为P2,
若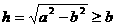 (如图1),则点M在线段AO上,
(如图1),则点M在线段AO上,
这时P到A、B、C三点的最远距离为
P1C和P2A,且P1C≥MC,P2A≥MA,所以点P与外心M
重合时,P到三镇的最远距离最小.
 若
若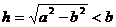 (如图2),则点M在线段AO外,这时
(如图2),则点M在线段AO外,这时
P到A、B、C三点的最远距离为P1C或P2A,
且P1C≥OC,P2A≥OC,所以点P与BC边中点O重合时,
P到三镇的最远距离最小为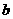 .
.
答:当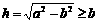 时,点P的位置在△ABC的外心
时,点P的位置在△ABC的外心
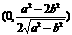 ;当
;当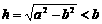 时,点P的位置在原点O.
时,点P的位置在原点O.
例8、某城市2001年末汽车保有量为30万辆,预计此后每年报废上一年末汽车保有量的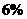 ,并且每年新增汽车数量相同。为保护城市环境,要求该城市汽车保有量不超过
,并且每年新增汽车数量相同。为保护城市环境,要求该城市汽车保有量不超过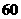 万量,那么每年新增汽车数量不应超过多少辆?
万量,那么每年新增汽车数量不应超过多少辆?
解:设2002年末汽车保有量为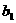 万辆,以后各年末汽车保有量依次为
万辆,以后各年末汽车保有量依次为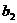 万辆,
万辆,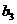 万辆……,每年新增汽车
万辆……,每年新增汽车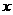 万辆,则
万辆,则
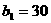 ,
,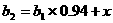
对于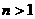 ,有
,有
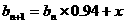
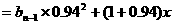
………………
∴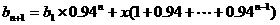
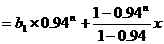
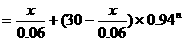
当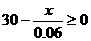 ,即
,即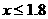 时,
时,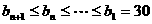
当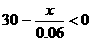 ,即
,即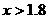 时,并且数列
时,并且数列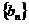 逐项增加,可以任意靠近
逐项增加,可以任意靠近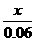
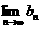

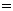
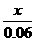
因此,如果要求汽车保有量不超过60万辆,即
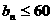
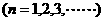
则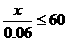 ,即
,即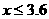 (万辆)
(万辆)
综上,每年新增汽车不应超过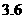 万辆。
万辆。
例9、 某服装厂生产一种服装,每件服装的成本为40元,出厂单价定为60元。该厂为鼓励销售商订购,决定当一次订购量超过100件时,每多订购一件,订购的全部服装的出厂单价就降低0.02元。根据市场调查,销售商一次订购量不会超过500件。
(I)设一次订购量为x件,服装的实际出厂单价为P元,写出函数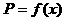 的表达式;
的表达式;
(II)当销售商一次订购了450件服装时,该服装厂获得的利润是多少元?
(服装厂售出一件服装的利润=实际出厂单价-成本)
本小题主要考查函数的基本知识,考查应用数学知识分析问题和解决问题的能力。
解:(I)当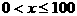 时,
时,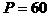
当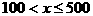 时,
时,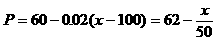
所以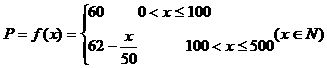
(II)设销售商的一次订购量为x件时,工厂获得的利润为L元,则
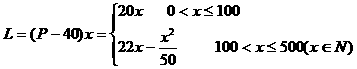
当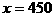 时,
时,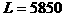
因此,当销售商一次订购了450件服装时,该厂获利的利润是5850元。
例10、本题共有2个小题,第一小题满分6分,第2小题满分8分.
某市2003年共有1万辆燃油型公交车。有关部门计划于2004年投入128辆电力型公交车,
随后电力型公交车每年的投入比上一年增加50%,试问:
(1) 该市在2010年应该投入多少辆电力型公交车?
(2) 到哪一年底,电力型公交车的数量开始超过该市公交车总量的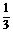 ?
?
解.(1)该市逐年投入的电力型公交车的数量组成等比数列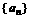 ,其中
,其中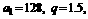
则在2010年应该投入的电力型公交车为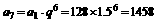 (辆)。
(辆)。
(2)记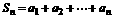 ,依据题意,得
,依据题意,得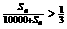 。于是
。于是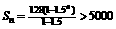 (辆),即
(辆),即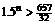 ,
,
则有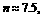 因此
因此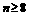 。所以,到2011年底,电力型公交车的数量开始超过该市公交车总量的
。所以,到2011年底,电力型公交车的数量开始超过该市公交车总量的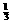 。
。
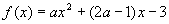 在区间
在区间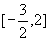 上的最大值为1,求实数a的值.
上的最大值为1,求实数a的值. 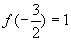 ,
,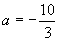 ,而顶点横坐标
,而顶点横坐标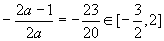 ,最大值在顶点外取得,故此解舍去.
当最大值为f(2)时,f(2)=1,
,最大值在顶点外取得,故此解舍去.
当最大值为f(2)时,f(2)=1,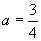 ,顶点在
,顶点在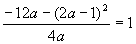 ,解得
,解得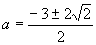 ,当
,当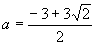 ,此时,顶点不在区间
,此时,顶点不在区间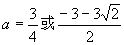 .
. 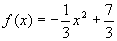 的定义域是[a,b],值域也是[a,b],求a.b的值.2)解:y=f(x)的图象如图,分三种情况讨论.
当a<b≤0时,f(x)为递增函数,有
的定义域是[a,b],值域也是[a,b],求a.b的值.2)解:y=f(x)的图象如图,分三种情况讨论.
当a<b≤0时,f(x)为递增函数,有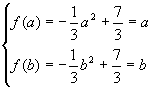 ,
解得,
,
解得,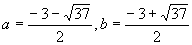 ,由于b>0,应舍去.
当0≤a<b时,f(x)为递减函数,
有
,由于b>0,应舍去.
当0≤a<b时,f(x)为递减函数,
有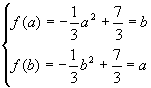 ,解得:a=1,b=2.
当a<0<b时,f(x)最大值在顶点处取得,故
,解得:a=1,b=2.
当a<0<b时,f(x)最大值在顶点处取得,故 ,
,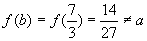 ,所以最小值应在a处取得. (2)解:y=f(x)的图象如图,分三种情况讨论.
当a<b≤0时,f(x)为递增函数,有
,所以最小值应在a处取得. (2)解:y=f(x)的图象如图,分三种情况讨论.
当a<b≤0时,f(x)为递增函数,有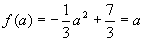 ,解得:
,解得: ,
综上,
,
综上,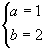 或
或 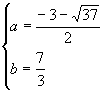 (3)求函数
(3)求函数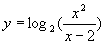 的最小值. 解(3)分析:由于对数的底已明确是2,所以只须求
的最小值. 解(3)分析:由于对数的底已明确是2,所以只须求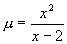 的最小值.
(3)解法一:∵
的最小值.
(3)解法一:∵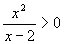 ,∴x>2.
设
,∴x>2.
设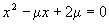 ,
由于该方程有实根,且实根大于2,
∴
,
由于该方程有实根,且实根大于2,
∴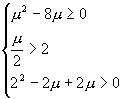 解之,μ≥8.
当μ=8时,x=4,故等号能成立.
于是log2≥0且x=4时,等号成立,因此
解之,μ≥8.
当μ=8时,x=4,故等号能成立.
于是log2≥0且x=4时,等号成立,因此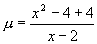 =
=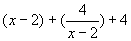
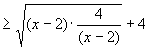 ∴μ≥8且
∴μ≥8且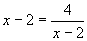 ,即x=4时,等号成立,
∴log2μ≥3且x=4时,等号成立.
故
,即x=4时,等号成立,
∴log2μ≥3且x=4时,等号成立.
故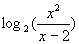 的最小值是3.
(4)已知a>0,a≠1,试求方程
的最小值是3.
(4)已知a>0,a≠1,试求方程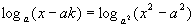 有解时k的取值范围. 4)解法一:原方程
有解时k的取值范围. 4)解法一:原方程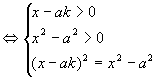
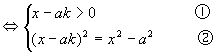 由②可得:
由②可得: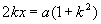 ③,
当k=0时,③无解,原方程无解;
当k≠0时,③解为
③,
当k=0时,③无解,原方程无解;
当k≠0时,③解为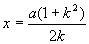 ,代入①式,
,代入①式,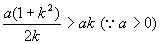
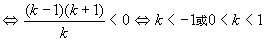 .
. 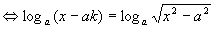 ,
原方程有解,应方程组
,
原方程有解,应方程组
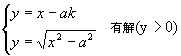 ,
即两曲线有交点,那么ak<-a或0<ak<a(a>0)
∴k<-1或0<k<1.
,
即两曲线有交点,那么ak<-a或0<ak<a(a>0)
∴k<-1或0<k<1.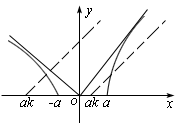 (5)设函数
(5)设函数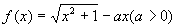 (Ⅰ)解不等式f(x)≤1
(Ⅱ)求a的取值范围,使f(x)在[0,+∞]上是单调函数.
(Ⅰ)解不等式f(x)≤1
(Ⅱ)求a的取值范围,使f(x)在[0,+∞]上是单调函数. 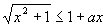 由此得:1≤1+ax即ax≥0,其中常数a>0,
∴原不等式
由此得:1≤1+ax即ax≥0,其中常数a>0,
∴原不等式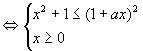 即
即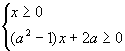 ∴当0<a<1时,所给不等式解集为
∴当0<a<1时,所给不等式解集为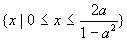 ,
当a≥1时,所给不等式解集为{x|x≥0}.
(Ⅱ)在区间[0,+∞)上任取x1,x2,使得x1<x2,
,
当a≥1时,所给不等式解集为{x|x≥0}.
(Ⅱ)在区间[0,+∞)上任取x1,x2,使得x1<x2,
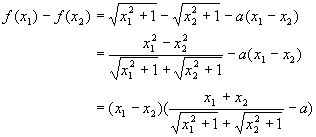 (ⅰ)当a≥1时,
∵
(ⅰ)当a≥1时,
∵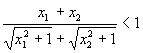 ∴
∴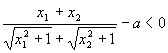 又
又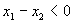 ∴
∴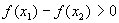 所以,当a≥1时,函数f(x)在区间[0,+∞)上是单调递减函数.
(ⅱ)当0<a<1时,在[0,+∞)上存在两点
所以,当a≥1时,函数f(x)在区间[0,+∞)上是单调递减函数.
(ⅱ)当0<a<1时,在[0,+∞)上存在两点 满足f(x1)=1,f(x2)=1 ,即f(x1)=f(x2),∴函数f(x)在区间[0,+∞)上不是单调函数.
满足f(x1)=1,f(x2)=1 ,即f(x1)=f(x2),∴函数f(x)在区间[0,+∞)上不是单调函数.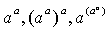 的大小.
分析:为比较aα与(aα) α的大小,将它们看成指数相同的两个幂,由于幂函数
的大小.
分析:为比较aα与(aα) α的大小,将它们看成指数相同的两个幂,由于幂函数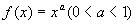 在区间[0,+∞]上是增函数,因此只须比较底数a与aα的大小,由于指数函数y=ax(0<a<1)为减函数,且1>a,所以a<aα,从而aα<(aα) α.
比较aα与(aα) α的大小,也可以将它们看成底数相同(都是aα)的两个幂,于是可以利用指数函数
在区间[0,+∞]上是增函数,因此只须比较底数a与aα的大小,由于指数函数y=ax(0<a<1)为减函数,且1>a,所以a<aα,从而aα<(aα) α.
比较aα与(aα) α的大小,也可以将它们看成底数相同(都是aα)的两个幂,于是可以利用指数函数 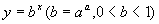 是减函数,由于1>a,得到aα<(aα) α.
由于a<aα,函数y=ax(0<a<1)是减函数,因此aα>(aα) α.
综上,
是减函数,由于1>a,得到aα<(aα) α.
由于a<aα,函数y=ax(0<a<1)是减函数,因此aα>(aα) α.
综上, 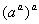
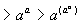 .
解以上两个例题的关键都在于适当地选取某一个函数,函数选得恰当,解决问题简单.
例3.关于x的方程
.
解以上两个例题的关键都在于适当地选取某一个函数,函数选得恰当,解决问题简单.
例3.关于x的方程 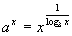 有实根,且根大于3,求实数a的范围.
分析:先将原方程化简为ax=3,但要注意0<x<3且x≠1.现将ax看成以a为底的指数函数,考虑底数a为何值时,函数值为3.如图(1),过(3,3)点的指数函数的底
有实根,且根大于3,求实数a的范围.
分析:先将原方程化简为ax=3,但要注意0<x<3且x≠1.现将ax看成以a为底的指数函数,考虑底数a为何值时,函数值为3.如图(1),过(3,3)点的指数函数的底 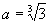 ,现要求0<x<3时,ax=3,所以
,现要求0<x<3时,ax=3,所以 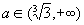 ,又因为x≠1,在图(1)中,过(1,3)点的指数函数的底a=3,所以
,又因为x≠1,在图(1)中,过(1,3)点的指数函数的底a=3,所以 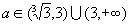 .
若将ax=3变形为
.
若将ax=3变形为 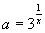 ,令
,令 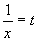 ,现研究指数函数a=3t,由0<x<1且x≠1,得
,现研究指数函数a=3t,由0<x<1且x≠1,得 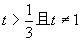 ,如图(2),很容易得到:
,如图(2),很容易得到: 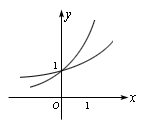
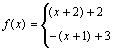
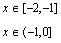 即
即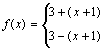
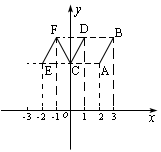
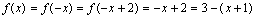 ,
于是在[–2,0]上,
,
于是在[–2,0]上, 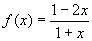 ,函数y=g(x)的图象与函数y=f-1(x+1)的图象关于y’=x对称,则g(5)=_____________-
解法一、由
,函数y=g(x)的图象与函数y=f-1(x+1)的图象关于y’=x对称,则g(5)=_____________-
解法一、由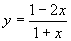 去分母,得
去分母,得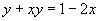 ,解出x,得
,解出x,得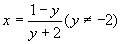 ,
故
,
故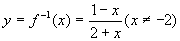 ,于是
,于是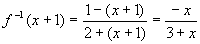 ,
设
,
设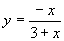 ,去分母得,
,去分母得,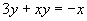 ,解出x,得
,解出x,得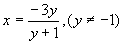 ,
∴
,
∴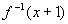 的反函数
的反函数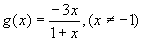 .
∴
.
∴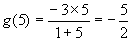 .
解法二、由
.
解法二、由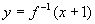 ,则
,则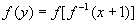 ,
∴
,
∴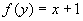 ,∴
,∴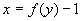 .
.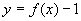 ,
, 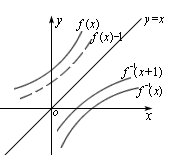 根据已知:
根据已知: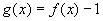 ∴
∴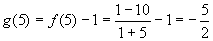 .
. 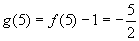 .
.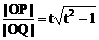 ,当t变化时,求点P轨迹。
,当t变化时,求点P轨迹。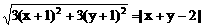 表示的曲线是
表示的曲线是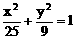 绕它的左焦点顺时针方向旋转
绕它的左焦点顺时针方向旋转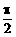 ,则所得新椭圆的准线方程是
,则所得新椭圆的准线方程是 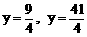 B、
B、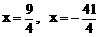 C、
C、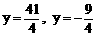 D、
D、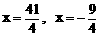
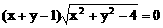 的曲线形状是
的曲线形状是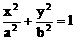 (a>b>0)的两焦点,过F1的弦AB与F2组成等腰直角三角形ABF2,其中∠BAF2=900,则椭圆的离心率是
(a>b>0)的两焦点,过F1的弦AB与F2组成等腰直角三角形ABF2,其中∠BAF2=900,则椭圆的离心率是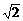 B、
B、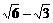 C、
C、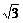 D、
D、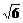
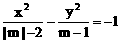 表示焦点在y轴上的双曲线,则它的半焦距C的取值范围是
表示焦点在y轴上的双曲线,则它的半焦距C的取值范围是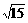 B、
B、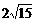 C、
C、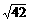 D、
D、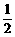 B、x2+y2=
B、x2+y2=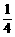 C、x2+y2=
C、x2+y2=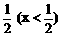 D、x2+y2=
D、x2+y2=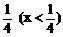
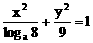 的离心率为
的离心率为