17.已知向量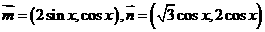 ,定义函数
,定义函数
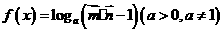 ,求函数
,求函数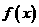 的最小正周期、单调递增区间.
的最小正周期、单调递增区间.
解:.因为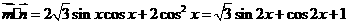
所以 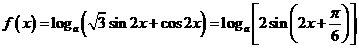 ,故
,故 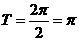 ,
,
令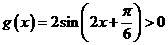 ,则
,则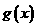 的单调递增的正值区间是
的单调递增的正值区间是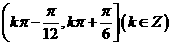 ,单调递减的正值区间是
,单调递减的正值区间是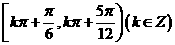 则当
则当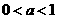 时,函数
时,函数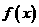 的单调递增区间为
的单调递增区间为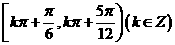
当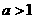 时,函数
时,函数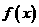 的单调递增区间为
的单调递增区间为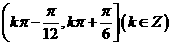
16.给出下列四个命题:①设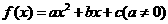 ,若
,若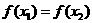
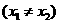 ,则
,则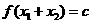 ;②若偶函数
;②若偶函数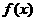 在
在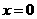 处可导,则
处可导,则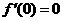 ; ③函数
; ③函数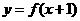 与
与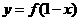 的图象关于直线
的图象关于直线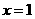 对称;④函数
对称;④函数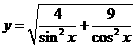 的最小值是 5.则其中错误的命题的序号是 .
的最小值是 5.则其中错误的命题的序号是 .
杭州二中高三代数质量检测题(五)答题卷
班级 姓名 学号
17.已知向量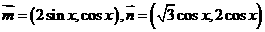 ,定义函数
,定义函数
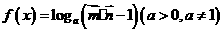 ,求函数
,求函数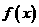 的最小正周期、单调递增区间.
的最小正周期、单调递增区间.
解:.因为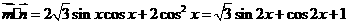
所以 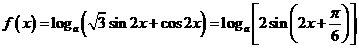 ,故
,故 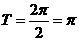 ,
,
令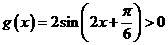 ,则
,则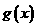 的单调递增的正值区间是
的单调递增的正值区间是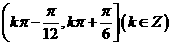 ,单调递减的正值区间是
,单调递减的正值区间是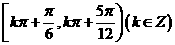 则当
则当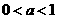 时,函数
时,函数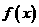 的单调递增区间为
的单调递增区间为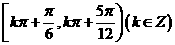
当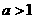 时,函数
时,函数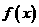 的单调递增区间为
的单调递增区间为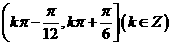
16.给出下列四个命题:①设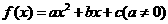 ,若
,若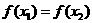
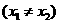 ,则
,则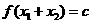 ;②若偶函数
;②若偶函数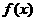 在
在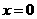 处可导,则
处可导,则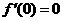 ; ③函数
; ③函数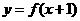 与
与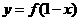 的图象关于直线
的图象关于直线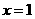 对称;④函数
对称;④函数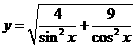 的最小值是 5.则其中错误的命题的序号是 .
的最小值是 5.则其中错误的命题的序号是 .
杭州二中高三代数质量检测题(五)答题卷
班级 姓名 学号