0 50928 50936 50942 50946 50952 50954 50958 50964 50966 50972 50978 50982 50984 50988 50994 50996 51002 51006 51008 51012 51014 51018 51020 51022 51023 51024 51026 51027 51028 51030 51032 51036 51038 51042 51044 51048 51054 51056 51062 51066 51068 51072 51078 51084 51086 51092 51096 51098 51104 51108 51114 51122 447348
 x2<a2
x2<a2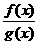 >0
>0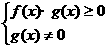
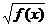 ≥g(x)
≥g(x) 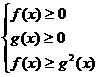 或
或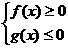
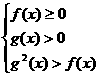
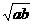 ”这类不等式,以及运用不等式性质所能完成的简单的不等式的证明。用数学归纳法证明与自然数有关命题的不等式难度较大。
”这类不等式,以及运用不等式性质所能完成的简单的不等式的证明。用数学归纳法证明与自然数有关命题的不等式难度较大。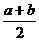 ≥
≥ ≥
≥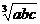 (当且仅当a=b=c时取“=”号)
(当且仅当a=b=c时取“=”号)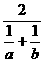 ≤
≤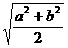
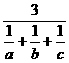 ≤
≤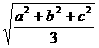
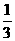 (a+b+c)2≥ab+bc+ca,a,b,c∈R(当且仅当a=b=c时等号成立)
(a+b+c)2≥ab+bc+ca,a,b,c∈R(当且仅当a=b=c时等号成立)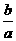 +
+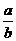 |≥2(当且仅当|a|=|b|时取“=”号)
|≥2(当且仅当|a|=|b|时取“=”号)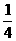 等。
等。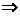 a>c(传递性)
a>c(传递性)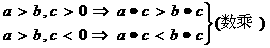
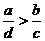
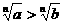 (n∈N)
(n∈N)
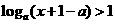 的解集为A,不等式
的解集为A,不等式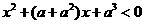 的解集为B,且
的解集为B,且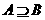 ,求实数
,求实数 的取值范围。
的取值范围。