0 50932 50940 50946 50950 50956 50958 50962 50968 50970 50976 50982 50986 50988 50992 50998 51000 51006 51010 51012 51016 51018 51022 51024 51026 51027 51028 51030 51031 51032 51034 51036 51040 51042 51046 51048 51052 51058 51060 51066 51070 51072 51076 51082 51088 51090 51096 51100 51102 51108 51112 51118 51126 447348
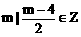 },N={x|
},N={x| ,则M∩N=__________。
,则M∩N=__________。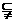 {1,2,3,4,5},(2)若元素a∈p,则6-a∈p,则集合p个数是__________。
{1,2,3,4,5},(2)若元素a∈p,则6-a∈p,则集合p个数是__________。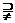 M D、M
M D、M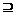 {a}
{a} B
B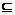 A
A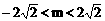
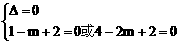 ,m无解
,m无解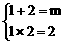
 ”、“
”、“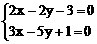 得1,2交点P(
得1,2交点P(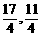 )
)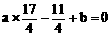
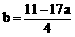
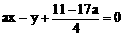
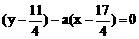
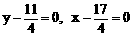 的交点(
的交点(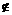 A},集合U表
A},集合U表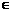 或
或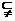 ,=表示,当A
,=表示,当A