0 50934 50942 50948 50952 50958 50960 50964 50970 50972 50978 50984 50988 50990 50994 51000 51002 51008 51012 51014 51018 51020 51024 51026 51028 51029 51030 51032 51033 51034 51036 51038 51042 51044 51048 51050 51054 51060 51062 51068 51072 51074 51078 51084 51090 51092 51098 51102 51104 51110 51114 51120 51128 447348
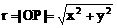 ,则
,则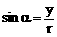 ,
,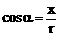 ,
,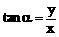 ,
,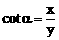 。
。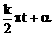 与α之间函数值关系(k∈Z),其规律是“奇变偶不变,符号看象限”;(2)同角三角函数关系式:平方关系,倒数关系,商数关系。
与α之间函数值关系(k∈Z),其规律是“奇变偶不变,符号看象限”;(2)同角三角函数关系式:平方关系,倒数关系,商数关系。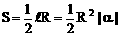 ,其中α为弧所对圆心角的弧度数。
,其中α为弧所对圆心角的弧度数。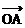 =(3,1),
=(3,1),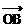 =(-1,2),
=(-1,2),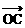 ⊥
⊥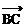 ∥
∥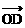 +
+ +
+ =(2,-8),
=(2,-8),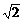 ,|
,|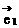 ,
,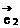 |是平面上一个基底,若
|是平面上一个基底,若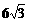 ,|
,|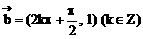 平移,得到函数___________的图象。
平移,得到函数___________的图象。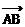 ∥
∥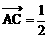
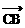 ,连DC并延长至E,使|
,连DC并延长至E,使|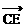 |=
|=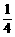 |
|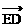 |,则点E坐标为:
|,则点E坐标为: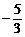 ) B、(
) B、(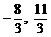 ) C、(0,1) D、(0,1)或(2,
) C、(0,1) D、(0,1)或(2,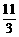 )
)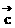 是任意的非零平面向量,且相互不共线,则:
是任意的非零平面向量,且相互不共线,则: |2中,真命题是:
|2中,真命题是: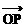 =
=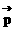 ,若
,若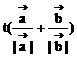 ,t∈R,则点P在
,t∈R,则点P在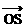 =(4,0),则
=(4,0),则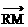 =
=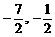 ) B、(
) B、(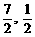 ) C、(7,4) D、(
) C、(7,4) D、(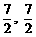 )
) 例1、如图,
例1、如图,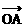 ,
,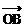 为单位向量,
为单位向量,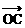 与
与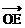 =λ
=λ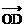 =μ
=μ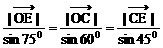 得:
得: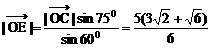
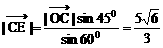
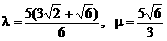
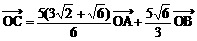
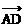 坐标。
坐标。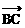 =(-6,-3),
=(-6,-3),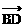 =(x-3,y-2),
=(x-3,y-2),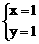
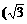 ,-1)和
,-1)和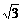 )夹角相等,且模为
)夹角相等,且模为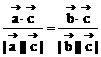
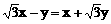
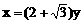 ①
①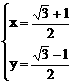 或
或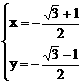 (舍)
(舍) ∴
∴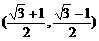
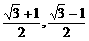 )
)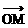 |∶|
|∶|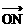 |∶|
|∶|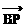 =s
=s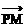
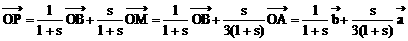 ①
①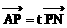
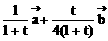 ②
②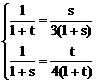 解之得:
解之得: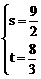
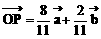
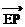 =(-1,y)
=(-1,y)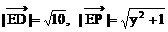
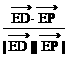
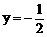 (舍),或y=2
(舍),或y=2 =(2,1),
=(2,1),