0 50948 50956 50962 50966 50972 50974 50978 50984 50986 50992 50998 51002 51004 51008 51014 51016 51022 51026 51028 51032 51034 51038 51040 51042 51043 51044 51046 51047 51048 51050 51052 51056 51058 51062 51064 51068 51074 51076 51082 51086 51088 51092 51098 51104 51106 51112 51116 51118 51124 51128 51134 51142 447348
 是定义在
是定义在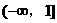 上的减函数,且对一切实数x,不等式
上的减函数,且对一切实数x,不等式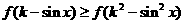 恒成立,求k的值。
恒成立,求k的值。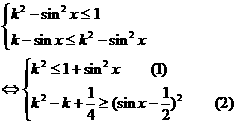
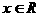 恒成立,则有
恒成立,则有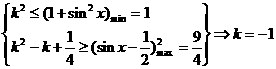
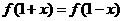 ,并且
,并且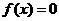 有三个实根,则这三个实根之和是_______。
有三个实根,则这三个实根之和是_______。 是函数
是函数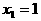 必是方程的一个根,其余两根
必是方程的一个根,其余两根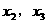 关于直线
关于直线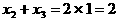 ,故
,故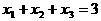 。
。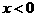 时,
时,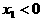 ,
,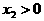 ,且
,且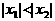 ,则
,则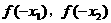 的大小关系是_______。
的大小关系是_______。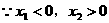 且
且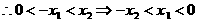
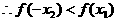
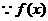 是偶函数,
是偶函数,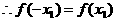
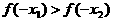
 ,且
,且 对一切正实数x,y都成立,若
对一切正实数x,y都成立,若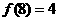 ,则
,则 _______。
_______。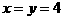 ,得
,得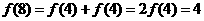 ,
,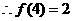
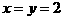 ,
,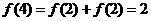 ,
,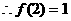
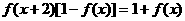 ,
,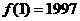 ,求
,求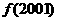 的值。
的值。 ,于是
,于是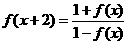 ,
,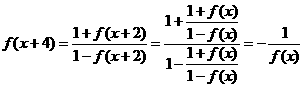
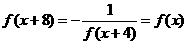
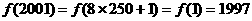
 ,并存在正实数c,使
,并存在正实数c,使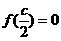 。试问
。试问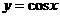 满足题设条件,且
满足题设条件,且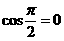 ,猜测
,猜测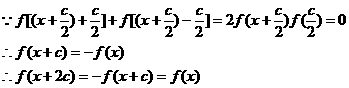
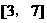 上是增函数且有最小值为5,那么
上是增函数且有最小值为5,那么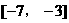 上是
上是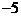 B.
增函数且最大值为
B.
增函数且最大值为
 上是减函数,问
上是减函数,问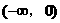 上是增函数还是减函数,并证明你的结论。
上是增函数还是减函数,并证明你的结论。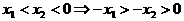
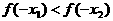 。
。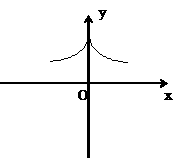 又
又 ,
, ,故
,故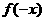 的关系。
的关系。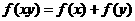 ,求证:
,求证: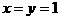 ,
,
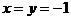 ,得
,得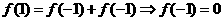
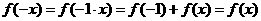
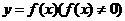 与
与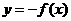 的图象关于原点对称,求证:函数
的图象关于原点对称,求证:函数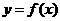 是偶函数。
是偶函数。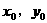 )
)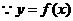 与
与 关于原点的对称点
关于原点的对称点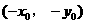 在
在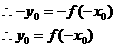
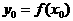
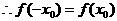
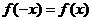 ,所以
,所以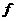 ”前的“负号”,三是利用函数单调性去掉函数符号“
”前的“负号”,三是利用函数单调性去掉函数符号“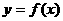 定义在R上,当
定义在R上,当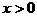 时,
时, ,且对任意
,且对任意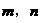 ,有
,有 ,当
,当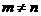 时
时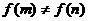 。
。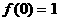 ;
;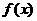 在R上是增函数;
在R上是增函数;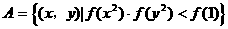 ,
,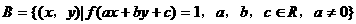 ,若
,若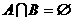 ,求
,求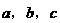 满足的条件。
满足的条件。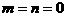 得
得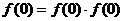 ,
,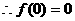 或
或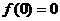 ,当
,当 时,有
时,有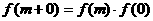 ,这与当
,这与当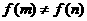 矛盾,
矛盾, 。
。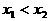 ,则
,则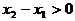 ,由已知得
,由已知得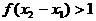 ,因为
,因为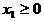 ,
,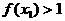 ,若
,若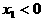 时,
时,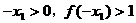 ,由
,由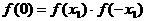
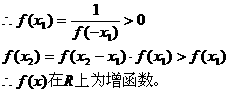
 得
得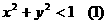
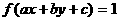 得
得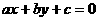 (2)
(2)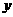 得
得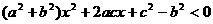 ,因为
,因为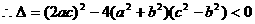 ,
,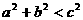
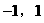 )上的函数
)上的函数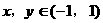 都有
都有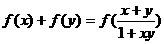 ,
,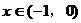 时,有
时,有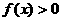 ,
,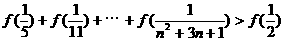 。
。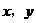 ,令
,令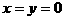 ,再令
,再令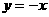 可得
可得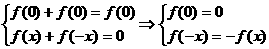 ,所以
,所以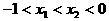 ,则
,则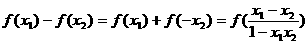
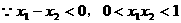 ,
,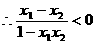 ,由条件(2)知
,由条件(2)知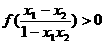 ,从而有
,从而有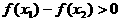 ,即
,即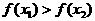 ,故
,故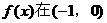 上单调递减,由奇函数性质可知,
上单调递减,由奇函数性质可知,
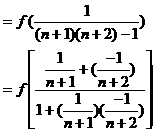
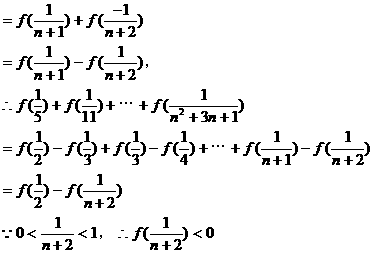
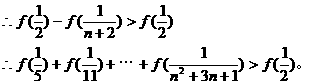
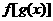 中的
中的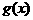 看作一个整体,相当于
看作一个整体,相当于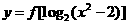 的定义域是___。
的定义域是___。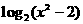 相当于
相当于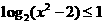 ,解得
,解得 或
或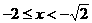 。
。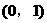 ,则
,则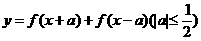 的定义域是______。
的定义域是______。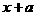 及
及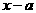 均相当于
均相当于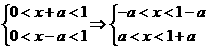
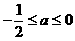 时,则
时,则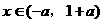
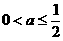 时,则
时,则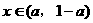
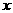 有
有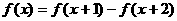 ,求证:
,求证: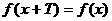 (T为非零常数)则
(T为非零常数)则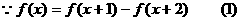
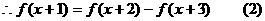
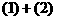 得
得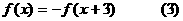
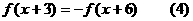
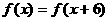 。
。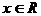 都成立,因此
都成立,因此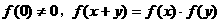 ,且当
,且当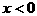 时,
时,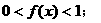 (2)
(2) 对一切
对一切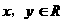 有
有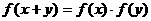 。
。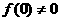 ,令
,令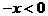 ,
,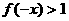 ,
,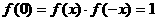
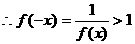
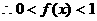 ,
,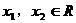 且
且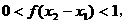
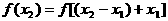

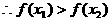 ,
,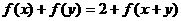 ,当
,当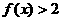 ,
,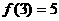 ,求不等式
,求不等式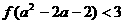 的解集。
的解集。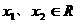 且
且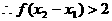 ,
,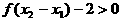 ,
,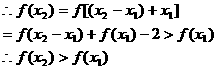
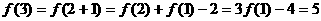
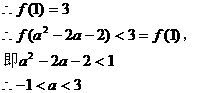
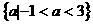 。
。