纵观近几年的新课程高考卷以及2004、2003年的江苏卷,函数的主干知识、知识的综合应用以及函数与方程思想等数学思想方法的考查,一直是高考的重点内容之一.在高考试卷上,与函数相关的试题所占比例始终在20%左右,且试题中既有灵活多变的客观性试题,又有一定能力要求的主观性试题.
(2004年,江苏卷8)若函数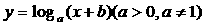 的图象过两点
的图象过两点
(-1,0)和(0,1),则
(A)a=2,b=2 (B)a=,b=2 (C)a=2,b=1 (D)a=,b=
(2003年,江苏卷6)函数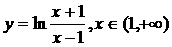 的反函数为
的反函数为
(A)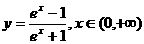 (B)
(B)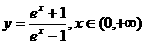
(C)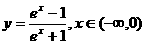 (D)
(D)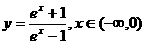
(2004年,江苏卷11)设k>1,f(x)=k(x-1)(x∈R) . 在平面直角坐标系xOy中,函数y=f(x)的图象与x轴交于A 点,它的反函数y=f -1(x)的图象与y轴交于B点,并且这两个函数的图象交于P点. 已知四边形OAPB的面积是3,则k等于
(A)3 (B) (C) (D)
(2003年,江苏卷9)已知方程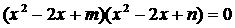 的四个根组成一个首项为
的四个根组成一个首项为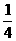 的等差数列,则 |m-n|=
的等差数列,则 |m-n|=
(A)1 (B)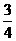 (C)
(C)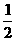 (D)
(D)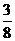
(2004年,江苏卷13)二次函数y=ax2+bx+c(x∈R)的部分对应值如下表:
|
x |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
4 |
|
y |
6 |
0 |
-4 |
-6 |
-6 |
-4 |
0 |
6 |
则不等式ax2+bx+c>0的解集是_______________________.
(2003年,江苏卷4)设函数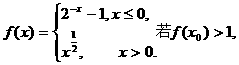 则x0的取值范围是
则x0的取值范围是
(A)(-1,1) (B)(-1,+∞)
(C)(-∞,-2)∪(0,+∞) (D)(-∞,-1)∪(1,+∞)
(2004年,江苏卷12)设函数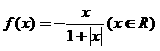 ,区间M=[a,b](a<b),集合N={
,区间M=[a,b](a<b),集合N={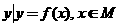 },则使M=N成立的实数对(a,b)有
},则使M=N成立的实数对(a,b)有
(A)0个 (B)1个 (C)2个 (D)无数多个
(2003年,江苏卷1)如果函数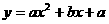 的图象与x轴有两个交点,则点(a,b)在aOb平面上的区域(不包含边界)为
的图象与x轴有两个交点,则点(a,b)在aOb平面上的区域(不包含边界)为

(2004年,江苏卷22)已知函数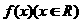 满足下列条件:对任意的实数x1,x2都有
满足下列条件:对任意的实数x1,x2都有 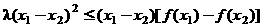
和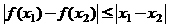 ,其中
,其中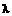 是大于0的常数.
是大于0的常数.
设实数a0,a,b满足
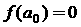 和
和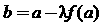
(Ⅰ)证明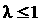 ,并且不存在
,并且不存在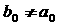 ,使得
,使得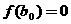 ;
;
(Ⅱ)证明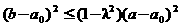 ;
;
(Ⅲ)证明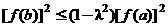 .
.
(2003年,江苏卷22) 设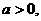 如图,已知直线
如图,已知直线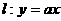 及曲线C:
及曲线C: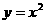 ,C上的点Q1的横坐标为
,C上的点Q1的横坐标为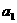 (
(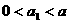 ).从C上的点Qn(n≥1)作直线平行于x轴,交直线
).从C上的点Qn(n≥1)作直线平行于x轴,交直线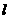 于点
于点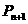 ,再从点
,再从点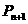 作直线平行于y轴,交曲线C于点Qn+1.
作直线平行于y轴,交曲线C于点Qn+1.
Qn (n=1,2,3,…)的横坐标构成数列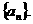
 (Ⅰ)试求
(Ⅰ)试求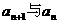 的关系,并求
的关系,并求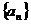 的通项公式;
的通项公式;
(Ⅱ)当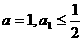 时,证明
时,证明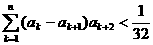 ;
;
(Ⅲ)当a=1时,证明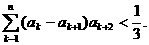
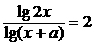 无解,则
无解,则 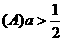
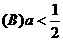
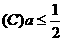
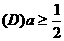
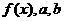 为任意正实数,且
为任意正实数,且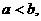 若
若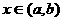 时,恒有
时,恒有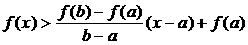 成立,则下列关系式中正确的是
成立,则下列关系式中正确的是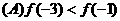
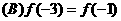
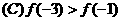
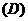 以上都不正确
以上都不正确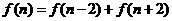 对一切大于1的正整数
对一切大于1的正整数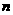 都成立,
都成立, 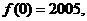 则
则
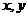 满足:
满足: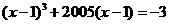 ,
,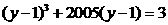 ,
,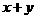 =
=
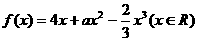 在区间[-1,1]上是增函数.
在区间[-1,1]上是增函数.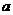 的值组成的集合A;
的值组成的集合A;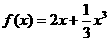 的两个非零实根为x1、x2.试问:是否存在实数m,使得不等式
的两个非零实根为x1、x2.试问:是否存在实数m,使得不等式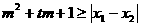 对任意
对任意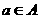 及
及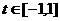 恒成立?若存在,求m的取值范围;若不存在,请说明理由.
恒成立?若存在,求m的取值范围;若不存在,请说明理由.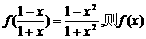 的解析式可取为
的解析式可取为  (B)
(B)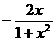 (C)
(C)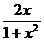 (D)
(D)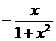
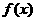 和g(x)都是定义在实数集R上的函数,且方程
和g(x)都是定义在实数集R上的函数,且方程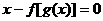 有实数解,则
有实数解,则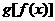 不可能是
不可能是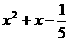 (B)
(B)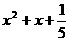 (C)
(C)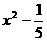 (D)
(D)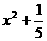
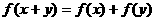 ②
②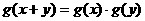
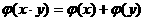 ④
④ 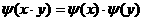
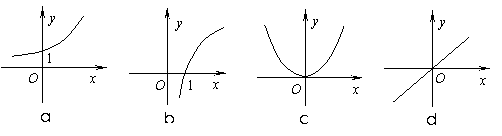
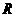 ,若
,若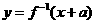 与
与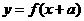 互为反函数且
互为反函数且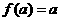 (
(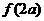 =
=
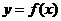 的定义域为
的定义域为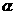 、
、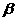 ,有:
,有: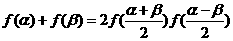 且
且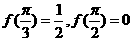
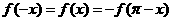
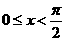 ,
,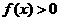 ,证明:
,证明: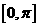 递减
递减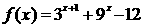 ,要使
,要使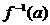 有意义,实数
有意义,实数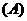
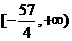
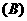
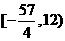

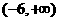
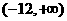
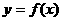 的图象可由函数
的图象可由函数 的图象绕坐标原点
的图象绕坐标原点 逆时针旋转
逆时针旋转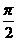 得到,则
得到,则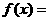
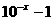
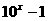
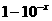
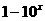
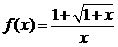 ,
,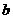 为两个不相等的正实数,则下列不等式正确的是
为两个不相等的正实数,则下列不等式正确的是 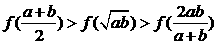 (B)
(B)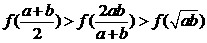
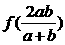
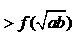
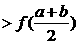 (D)
(D)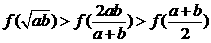
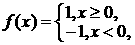 则不等式
则不等式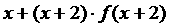 ≤5的解集是
.
≤5的解集是
.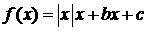 ,有下列命题:①
,有下列命题:①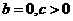 时,
时,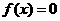 只有一个实数根②
只有一个实数根②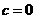 时,
时,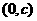 对称④方程
对称④方程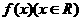 为奇函数,
为奇函数,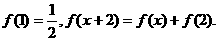 则
则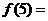
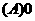
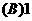
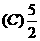
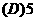
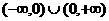 的函数
的函数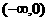 上是增函数,若
上是增函数,若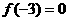 ,则
,则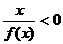 的解集是
的解集是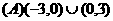
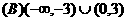
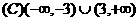
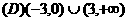
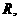 且
且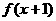 为奇函数,当
为奇函数,当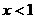 时,
时,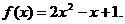 则当
则当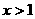 时,
时,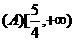
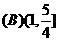
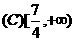
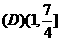
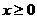 时,
时,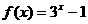 ,设
,设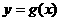 ,则
,则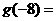
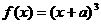 对任意实数
对任意实数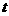 ,都有
,都有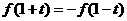 ,则
,则