0 50908 50916 50922 50926 50932 50934 50938 50944 50946 50952 50958 50962 50964 50968 50974 50976 50982 50986 50988 50992 50994 50998 51000 51002 51003 51004 51006 51007 51008 51010 51012 51016 51018 51022 51024 51028 51034 51036 51042 51046 51048 51052 51058 51064 51066 51072 51076 51078 51084 51088 51094 51102 447348
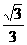 B.
B.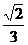 C.
C.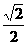 D.
D.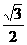


 X∥Y”为真命题的是_________(填序号).
X∥Y”为真命题的是_________(填序号). 平面BCE,MN在平面BCE外,
平面BCE,MN在平面BCE外,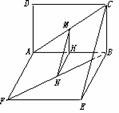
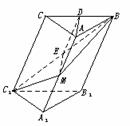 [例2]在斜三棱柱A1B1C1-ABC中,底面是等腰三角形,AB=AC,侧面BB1C1C⊥底面ABC.
[例2]在斜三棱柱A1B1C1-ABC中,底面是等腰三角形,AB=AC,侧面BB1C1C⊥底面ABC.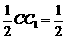 AA1,∴AM=MA1.
AA1,∴AM=MA1.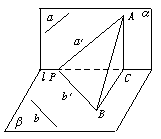 解析:如图,在l上任取一点P,过P分别在α、β内作a′∥a,b′∥b,在a′上任取一点A,过A作AC⊥l,垂足为C,则AC⊥β,过C作CB⊥b′交b′于B,连AB,由三垂线定理知AB⊥b′,∴△APB为直角三角形,故∠APB为锐角.
解析:如图,在l上任取一点P,过P分别在α、β内作a′∥a,b′∥b,在a′上任取一点A,过A作AC⊥l,垂足为C,则AC⊥β,过C作CB⊥b′交b′于B,连AB,由三垂线定理知AB⊥b′,∴△APB为直角三角形,故∠APB为锐角.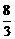 B.
B.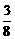 C.
C.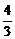 D.
D.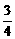
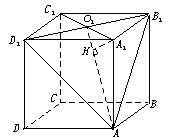 即是点A1到平面AB1D1的距离,在Rt△A1O1A中,A1O1=
即是点A1到平面AB1D1的距离,在Rt△A1O1A中,A1O1=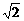 ,AO1=3
,AO1=3